|
|
|
|
| Beispiel | |
|
(3,5), (5,7), (11,13), (17,19), (29,31), (41,43), (59,61), (71,73),
(101,103) sind Primzahlzwillinge.
| |
2. Primzahldrillinge:
Man spricht von Primzahldrillingen , wenn unter vier aufeinanderfolgenden ungeraden
Zahlen drei Primzahlen sind.
| Beispiel | |
|
(5,7,11), (7,11,13), (11,13,17), (13,17,19), (17,19,23), (37,41,43) sind
Primzahldrillinge. | |
3. Primzahlvierlinge:
Bilden von fünf aufeinanderfolgenden ungeraden Zahlen die ersten beiden und die letzten
beiden jeweils einen Primzahlzwilling, dann spricht man von
Primzahlvierlingen .
| Beispiel | |
|
(5,7,11,13), (11,13,17,19), (101,103,107,109), (191,193,197,199) sind
Primzahlvierlinge.
| |
Eine bis heute unbewiesene Vermutung ist, daß unendlich viele Primzahlzwillinge,
unendlich viele Primzahldrillinge und unendlich viele Primzahlvierlinge existieren.
4. Mersennesche Primzahlen
Ist eine Zahl ![]() mit
mit ![]() eine Primzahl, dann ist auch
eine Primzahl, dann ist auch ![]() eine Primzahl.
Man nennt die Zahlen
eine Primzahl.
Man nennt die Zahlen ![]() (
(![]() Primzahl) MERSENNEsche Zahlen .
Von einer MERSENNEschen Primzahl spricht man, wenn
Primzahl) MERSENNEsche Zahlen .
Von einer MERSENNEschen Primzahl spricht man, wenn ![]() eine Primzahl
ist.
eine Primzahl
ist.
| Beispiel | |
|
Für die folgenden ersten 10 Werte von | |
5. Fermatsche Primzahlen
Ist eine Zahl ![]() mit
mit ![]() eine ungerade Primzahl, dann ist
eine ungerade Primzahl, dann ist ![]() eine
Potenz von
eine
Potenz von ![]() .
Die Zahlen
.
Die Zahlen ![]() mit
mit ![]() heißen FERMATsche Zahlen .
Ist eine FERMATsche Zahl eine Primzahl, dann spricht man von einer
FERMATschen Primzahl.
heißen FERMATsche Zahlen .
Ist eine FERMATsche Zahl eine Primzahl, dann spricht man von einer
FERMATschen Primzahl.
| Beispiel | |
|
Für | |
6. Fundamentalsatz der elementaren Zahlentheorie
Jede natürliche Zahl ![]() kann man als Produkt von Primzahlen darstellen.
Diese Darstellung ist eindeutig bis auf die Reihenfolge der Faktoren.
Man sagt, daß
kann man als Produkt von Primzahlen darstellen.
Diese Darstellung ist eindeutig bis auf die Reihenfolge der Faktoren.
Man sagt, daß ![]() genau eine Primfaktorenzerlegung besitzt.
genau eine Primfaktorenzerlegung besitzt.
| Beispiel | |
|
| |
Hinweis: Analog kann man ganze Zahlen (außer -1, 0, 1) eindeutig bis auf
Vorzeichen und Reihenfolge der Faktoren als Produkt von Primelementen darstellen.
7. Kanonische Primfaktorenzerlegung
Es ist üblich, in der Primfaktorenzerlegung einer natürlichen Zahl die Primfaktoren
der Größe nach zu ordnen und gleiche Faktoren zu Potenzen zusammenzufassen.
Ordnet man jeder nicht vorkommenden Primzahl den Exponenten 0 zu, dann gilt: Jede
natürliche Zahl ist eindeutig durch die Folge der Exponenten in ihrer
Primfaktorenzerlegung bestimmt.
| Beispiel | |
|
Zu | |
Für eine natürliche Zahl ![]() seien
seien ![]() die paarweise verschiedenen
die paarweise verschiedenen
![]() teilenden Primzahlen, und
teilenden Primzahlen, und ![]() bezeichne den Exponenten der Primzahl
bezeichne den Exponenten der Primzahl ![]() in
der Primfaktorenzerlegung von
in
der Primfaktorenzerlegung von ![]() .
Dann schreibt man
.
Dann schreibt man
| (5.246b) |
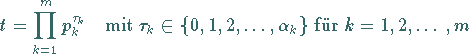 |
(5.247a) |
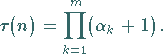 |
(5.247b) |
| Beispiel A | |
|
| |
| Beispiel B | |
|
| |
Das Produkt ![]() aller positiven Teiler von
aller positiven Teiler von ![]() ist gegeben durch
ist gegeben durch
| (5.247c) |
| Beispiel A | |
|
| |
| Beispiel B | |
|
| |
| Beispiel C | |
|
| |
Die Summe ![]() aller positiven Teiler von
aller positiven Teiler von ![]() ist
ist
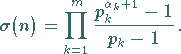 |
(5.247d) |
| Beispiel A | |
|
| |
| Beispiel B | |
|
| |
|
|
|