|
Im Zusammenhang mit FOURIER-Reihen werden Funktionen der
Form 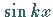 und
und 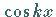 betrachtet.
Diese Funktionen können als Elemente von
betrachtet.
Diese Funktionen können als Elemente von 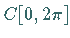 aufgefaßt werden.
Im Funktionenraum
aufgefaßt werden.
Im Funktionenraum 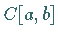 wird durch
wird durch
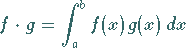 |
(5.224) |
ein Skalarprodukt erklärt.
Wegen
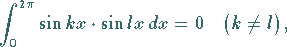 |
(5.225) |
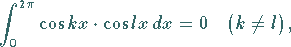 |
(5.226) |
 |
(5.227) |
sind die Funktionen 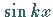 und
und 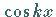 für alle
für alle 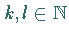 paarweise zueinander
orthogonal.
Diese Orthogonalität trigonometrischer Funktionen wird zur Berechnung der
FOURIER-Koeffizienten bei der FOURIER-Analyse
ausgenutzt.
paarweise zueinander
orthogonal.
Diese Orthogonalität trigonometrischer Funktionen wird zur Berechnung der
FOURIER-Koeffizienten bei der FOURIER-Analyse
ausgenutzt.
|