Unterräume, Dimensionsformel
1. Unterraum:
Es sei 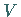 ein Vektorraum und
ein Vektorraum und 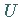 eine Teilmenge von
eine Teilmenge von 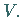 Bildet
Bildet 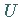 bezüglich der Operationen aus
bezüglich der Operationen aus 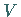 einen Vektorraum, so heißt
einen Vektorraum, so heißt 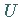 ein
Unterraum von
ein
Unterraum von 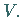
Eine nichtleere Teilmenge 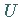 von
von 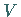 ist genau dann Unterraum, wenn für alle
ist genau dann Unterraum, wenn für alle
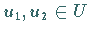 und alle
und alle 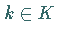 auch
auch 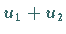 und
und 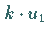 in
in 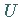 liegen
( Unterraumkriterium ).
liegen
( Unterraumkriterium ).
2. Kern, Bild: Es seien 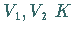 -Vektorräume.
Ist
-Vektorräume.
Ist 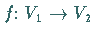 eine lineare Abbildung, so sind die Unterräume
Kern (Bezeichnung: ker
eine lineare Abbildung, so sind die Unterräume
Kern (Bezeichnung: ker  )
und Bild (Bezeichnung: im
)
und Bild (Bezeichnung: im  )
wie
folgt definiert:
)
wie
folgt definiert:
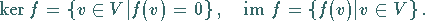 |
(5.217) |
So ist zum Beispiel die Lösungsmenge eines homogenen linearen Gleichungssystems
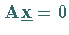 der Kern der durch die Koeffizientenmatrix
der Kern der durch die Koeffizientenmatrix 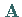 vermittelten linearen Abbildung.
vermittelten linearen Abbildung.
3. Dimension: Die Dimension 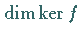 bzw.
bzw.  im
im  werden
Defekt
werden
Defekt  bzw. Rang
bzw. Rang  genannt.
Zwischen diesen Dimensionen besteht der Zusammenhang
genannt.
Zwischen diesen Dimensionen besteht der Zusammenhang
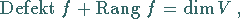 |
(5.218) |
der Dimensionsformel genannt wird.
Ist speziell Defekt 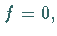 d.h.
d.h. 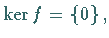 dann ist die lineare Abbildung
dann ist die lineare Abbildung
 injektiv und umgekehrt.
Injektive lineare Abbildungen werden regulär genannt.
injektiv und umgekehrt.
Injektive lineare Abbildungen werden regulär genannt.