Spinmultipletts
Die Spinfunktionen eines Teilchens mit der Spinquantenzahl 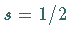 transformieren
sich nach der Darstellung
transformieren
sich nach der Darstellung 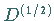 der Gruppe
der Gruppe 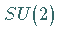 mit der Dimension
mit der Dimension
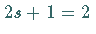 .
Das höchste Gewicht ist
.
Das höchste Gewicht ist 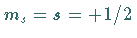 .
Darüberhinaus enthält der Darstellungsraum nur noch den Basiszustand mit dem
Gewicht
.
Darüberhinaus enthält der Darstellungsraum nur noch den Basiszustand mit dem
Gewicht 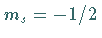 ,
so daß der Teilchenspin
,
so daß der Teilchenspin 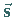 nur zwei
Einstellungsmöglichkeiten auf die Quantisierungsachse besitzt,
nur zwei
Einstellungsmöglichkeiten auf die Quantisierungsachse besitzt,
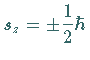 .
Der Betrag des Spins wird durch den Eigenwert des CASIMIR-Operators der
LIE-Algebra
.
Der Betrag des Spins wird durch den Eigenwert des CASIMIR-Operators der
LIE-Algebra 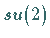 bestimmt:
bestimmt:
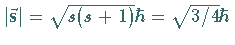 .
.
Die Spinfunktion zweier Teilchen mit dem Spin 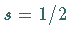 transformieren sich nach der
Produktdarstellung
transformieren sich nach der
Produktdarstellung 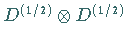 .
Bei einer geeigneten Basistransformation im vierdimensionalen Produktraum zerfällt
diese Darstellung in zwei irreduzible Darstellungen mit dem Gesamtspin
.
Bei einer geeigneten Basistransformation im vierdimensionalen Produktraum zerfällt
diese Darstellung in zwei irreduzible Darstellungen mit dem Gesamtspin 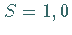 :
:
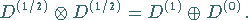 |
(5.194) |
Es ergibt sich ein Spintriplett 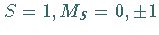 und ein Spinsingulett
und ein Spinsingulett
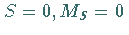 .
.
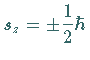 .
Der Betrag des Spins wird durch den Eigenwert des CASIMIR-Operators der
LIE-Algebra
.
Der Betrag des Spins wird durch den Eigenwert des CASIMIR-Operators der
LIE-Algebra