Gitterstrukturen
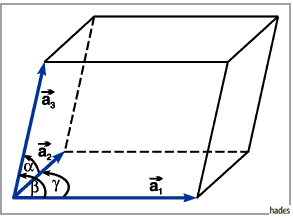
In der Kristallographie wird das Parallelepiped, das unabhängig von der Art
der Besetzung durch Atome oder Ionen die Elementarzelle eines Kristallgitters
darstellt, durch drei, von einem gewählten Gitterpunkt ausgehende nichtkomplanare
Basisvektoren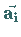 
bestimmt.
Die unendliche geometrische Gitterstruktur ergibt sich durch Ausführung aller
primitiven Translationen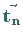 
:
 |
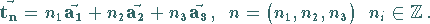(5.181) |
Dabei durchlaufen die Koeffizienten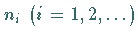 
alle ganzen
Zahlen.
Die Gesamtheit aller Translationen 
,
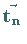die als Gittervektoren
die Raumpunkte des Gitters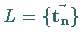 
festlegen, bilden die
Translationsgruppe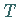 
mit dem Gruppenelement 
,
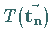dem
inversen Element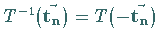 
und der
Multiplikationsregel
.
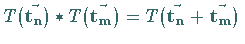Für die Anwendung eines Gruppenelementes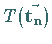 
auf den Ortsvektor
gilt:
 |
(5.182) |
