Symmetriegruppen
Zu jeder Symmetrieoperation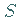 
gibt es eine inverse Operation 
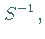die
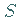wieder
,,rückgängig`` macht, d.h., es gilt
 |
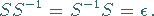(5.178) |
Dabei bezeichnet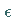 
die identische Operation, die den gesamten Raum unverändert
läßt.
Die Gesamtheit der Symmetrieoperationen eines räumlichen Objektes bildet bezüglich
der Hintereinander-Ausführung eine Gruppe, die im allgemeinen nichtkommutative
Symmetriegruppe des Objektes.
Dabei gelten die folgenden Beziehungen:
a) Jede Drehung ist das Produkt zweier Spiegelungen.
Die Schnittgerade der beiden Spiegelungsebenen ist die Drehachse.
b) Für zwei Spiegelungen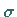 
und 
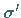gilt
 |
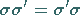(5.179) |
genau dann, wenn die zugehörigen Spiegelungsebenen identisch sind oder senkrecht
aufeinander stehen.
Im ersten Fall ist das Produkt die Identität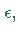 
im zweiten die Drehung
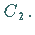
c) Das Produkt zweier Drehungen mit sich schneidenden Drehachsen ist wieder
eine Drehung, deren Achse durch den Schnittpunkt der gegebenen Drehachsen geht.
d) Für zwei Drehungen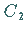 
und 
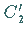um dieselbe oder um zwei zueinander
senkrechte Achsen gilt:
 |
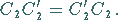(5.180) |
Das Produkt ist jeweils wieder eine Drehung.
Im ersten Fall ist die zugehörige Drehachse die gegebene, im zweiten steht die
Drehachse senkrecht auf den beiden gegebenen.
