Rechenregeln für Matrizen
Die folgenden Regeln können nur angewendet werden, wenn die darin auftretenden
Rechenoperationen durchführbar sind.
1. Die Multiplikation einer Matrix mit der Einheitsmatrix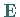 
wird wegen
 |
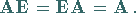(4.33) |
auch identische Abbildung genannt.
2. Multiplikationen einer Matrix 
mit der Skalarmatrix 
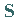oder
mit der Einheitsmatrix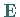
sind kommutativ:
 |
(4.34a) |
mit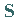
gemäß (4.8),
|
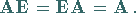(4.34b) |
3. Multiplikation einer Matrix mit der Nullmatrix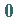 
ergibt die Nullmatrix:
 |
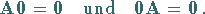(4.35) |
Die Umkehrung dieser Regel gilt im allgemeinen nicht, d.h., aus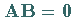 
folgt nicht notwendig 
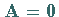oder 
.
4. Verschwindendes Produkt zweier Matrizen
Auch wenn weder
noch 
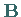Nullmatrizen sind, kann ihr Produkt eine
Nullmatrix ergeben:
 |
(4.36) |
| Beispiel |
|
|
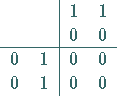
5. Multiplikation dreier Matrizen:
 |
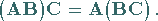(4.37) |
6. Transposition von Summe und Produkt zweier Matrizen:
 |
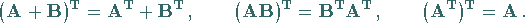(4.38a) |
Für quadratische Matrizen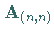 
gilt außerdem:
 |
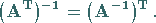(4.38b) |
7. Inverse eines Produkts aus zwei Matrizen:
 |
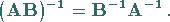(4.39) |
8. Potenzieren von Matrizen:
 |
(4.40a) |
 |
(4.40b) |
 |
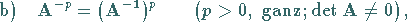(4.40c) |
 |
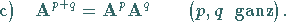(4.40d) |
9. Kronecker-Produkt:
Als KRONECKER-Produkt zweier Matrizen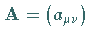 
und
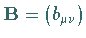bezeichnet man die Vorschrift
 |
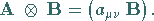(4.41) |
Bezüglich Transposition und Spur gelten die Regeln
 |
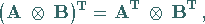(4.42) |
 |
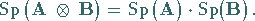(4.43) |
