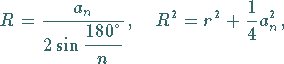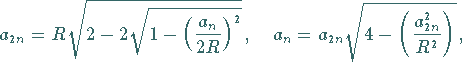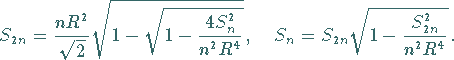Regelmäßige konvexe Vielecke haben 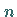 gleiche Seiten und
gleiche Seiten und 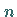 gleiche Innenwinkel.
Der Schnittpunkt der Mittellote der Seiten des Vielecks ist der Mittelpunkt
gleiche Innenwinkel.
Der Schnittpunkt der Mittellote der Seiten des Vielecks ist der Mittelpunkt 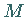 des einbeschriebenen und des umbeschriebenen Kreises mit den Radien
des einbeschriebenen und des umbeschriebenen Kreises mit den Radien 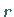 bzw.
bzw.
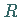 .
Die Seiten des
.
Die Seiten des  -Ecks sind Tangenten des Inkreises und Sehnen des Umkreises.
Sie bilden um den Inkreis das Tangentenvieleck , im Umkreis das
Sehnenvieleck .
-Ecks sind Tangenten des Inkreises und Sehnen des Umkreises.
Sie bilden um den Inkreis das Tangentenvieleck , im Umkreis das
Sehnenvieleck .
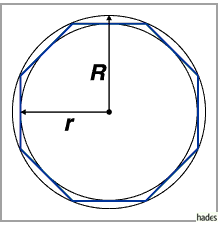
Die Zerlegung eines regelmäßigen konvexen  -Ecks ergibt
-Ecks ergibt  gleichschenklige
kongruente Dreiecke um den Mittelpunkt
gleichschenklige
kongruente Dreiecke um den Mittelpunkt 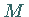 ,
die Bestimmungsdreiecke .
,
die Bestimmungsdreiecke .
Die Elemente des 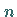 -Ecks werden im folgenden durch den Index
-Ecks werden im folgenden durch den Index 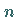 ,
die des
,
die des
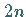 -Ecks mit dem Index
-Ecks mit dem Index 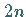 gekennzeichnet.
gekennzeichnet.
Für regelmäßige konvexe 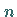 -Ecke gelten die folgenden Beziehungen.
-Ecke gelten die folgenden Beziehungen.
Zentriwinkel:
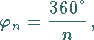 |
(3.50) |
Basiswinkel:
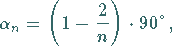 |
(3.51) |
Außenwinkel:
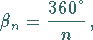 |
(3.52) |
Innenwinkel:
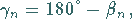 |
(3.53) |
Umkreisradius:
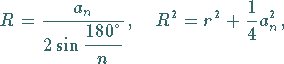 |
(3.54) |
Inkreisradius:
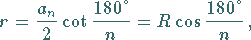 |
(3.55) |
Umfang:
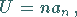 |
(3.56) |
Seitenlänge:
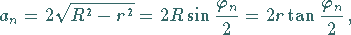 |
(3.57) |
Flächeninhalt:
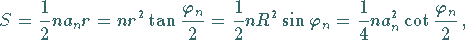 |
(3.58) |
Beziehungen zwischen Seitenlängen und Flächeninhalten von
n-Eck und 2n-Eck:
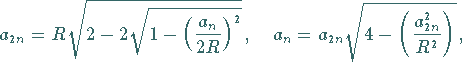 |
(3.59) |
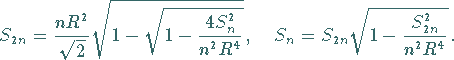 |
(3.60) |
![]() gleiche Seiten und
gleiche Seiten und ![]() gleiche Innenwinkel.
Der Schnittpunkt der Mittellote der Seiten des Vielecks ist der Mittelpunkt
gleiche Innenwinkel.
Der Schnittpunkt der Mittellote der Seiten des Vielecks ist der Mittelpunkt ![]() des einbeschriebenen und des umbeschriebenen Kreises mit den Radien
des einbeschriebenen und des umbeschriebenen Kreises mit den Radien ![]() bzw.
bzw.
![]() .
Die Seiten des
.
Die Seiten des ![]() -Ecks sind Tangenten des Inkreises und Sehnen des Umkreises.
Sie bilden um den Inkreis das Tangentenvieleck , im Umkreis das
Sehnenvieleck .
-Ecks sind Tangenten des Inkreises und Sehnen des Umkreises.
Sie bilden um den Inkreis das Tangentenvieleck , im Umkreis das
Sehnenvieleck .