Sehnenviereck
Ein Viereck, das von einem Umkreis umbeschrieben werden kann, heißt
Sehnenviereck , weil die Seiten dieses Vierecks Sehnen des Umkreises sind.
Ein Sehnenviereck liegt dann und nur dann vor, wenn die Summe zweier Gegenwinkel
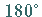 beträgt:
beträgt:
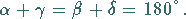 |
(3.39) |
Der Umkreisradius des Sehnenvierecks beträgt
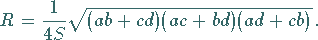 |
(3.40) |
Die Diagonalen berechnen sich gemäß
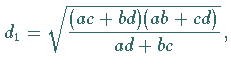 |
|
|
(3.41a) |
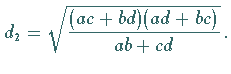 |
|
|
(3.41b) |
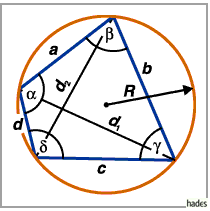
Für das Sehnenviereck gilt der Satz des PTOLEMÄUS :
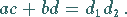 |
(3.42) |
Mit dem halben Umfang des Sehnenvierecks 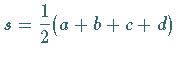 berechnet
sich sein Flächeninhalt gemäß
berechnet
sich sein Flächeninhalt gemäß
 |
(3.43) |
Ist das Sehnenviereck gleichzeitig ein Tangentenviereck, dann gilt
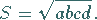 |
(3.44) |
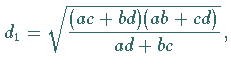
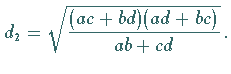
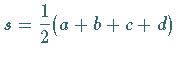 berechnet
sich sein Flächeninhalt gemäß
berechnet
sich sein Flächeninhalt gemäß