Messungen auf der Raumfläche
1. Länge des Bogens:
Die Länge einer Kurve 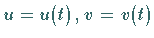 auf der Fläche wird für
auf der Fläche wird für
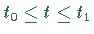 über
über
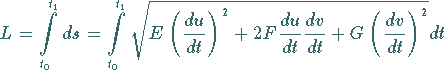 |
(3.524) |
berechnet.
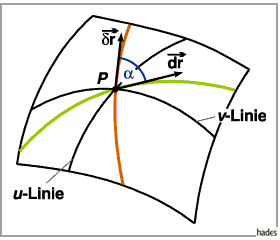
2. Winkel zwischen zwei Kurven:
Der Winkel zwischen zwei Kurven
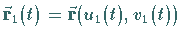 und
und 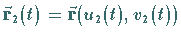 auf der Fläche
auf der Fläche 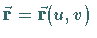 ,
d.h. zwischen ihren Tangenten,
die sich im Punkt
,
d.h. zwischen ihren Tangenten,
die sich im Punkt  schneiden und in diesem Punkt die durch die Vektoren
schneiden und in diesem Punkt die durch die Vektoren
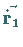 und
und 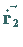 vorgegebene Richtung haben, wird mit
der Formel
vorgegebene Richtung haben, wird mit
der Formel
berechnet.
Die Koeffizienten 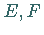 und
und 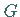 sind für den Punkt
sind für den Punkt  zu
bestimmen, und
zu
bestimmen, und
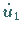 ,
,
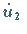 ,
,
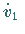 ,
,
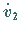 stellen die ersten
Ableitungen von
stellen die ersten
Ableitungen von 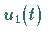 ,
,
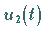 ,
,
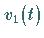 und
und 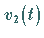 für den, dem
Punkt
für den, dem
Punkt  entsprechenden Parameterwert dar.
Wenn der Zähler von (3.525) verschwindet stehen beide Kurven
senkrecht aufeinander.
Die Orthogonalitätsbedingung für die Koordinatenlinien
entsprechenden Parameterwert dar.
Wenn der Zähler von (3.525) verschwindet stehen beide Kurven
senkrecht aufeinander.
Die Orthogonalitätsbedingung für die Koordinatenlinien 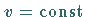 und
und
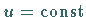 lautet
lautet 
3. Flächeninhalt eines Flächenstückes:
Der Flächeninhalt eines Flächenstückes 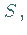 das von einer beliebigen, auf der
Fläche liegenden Kurve begrenzt wird, kann über das Doppelintegral
das von einer beliebigen, auf der
Fläche liegenden Kurve begrenzt wird, kann über das Doppelintegral
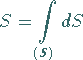 |
(3.526a) |
mit
 |
(3.526b) |
berechnet werden.
Man nennt 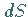 Flächenelement .
Flächenelement .
Die Berechnung von Längen, Winkeln und Flächeninhalten auf Flächen ist mit Hilfe
der Formeln (3.524, 3.525, 3.526a,b) möglich, wenn die
Koeffizienten 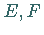 und
und 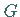 der ersten quadratischen Fundamentalform bekannt sind.
Somit definiert die erste quadratische Fundamentalform
die Metrik auf der Fläche .
der ersten quadratischen Fundamentalform bekannt sind.
Somit definiert die erste quadratische Fundamentalform
die Metrik auf der Fläche .