Asymptoten der Hyperbel
Asymptoten der Hyperbel sind Geraden, die sich den Hyperbelzweigen für
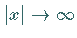unbegrenzt nähern
(s. Definition der Asymptoten).
Der Richtungskoeffizient der Asymptoten ist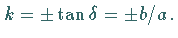 
Die Gleichungen der Asymptoten lauten
 |
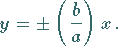(3.356) |
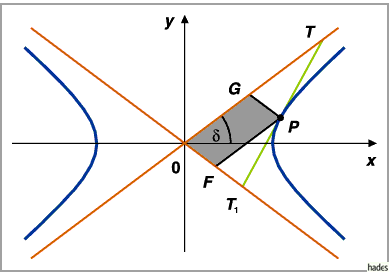
Die Asymptoten bilden gemeinsam mit der Tangente an die Hyperbel in einem Punkt
das Tangentenstück der Hyperbel , d.h. die Strecke
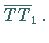Das Tangentenstück wird durch den Berührungspunkt
halbiert, so daß
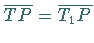ist.
Der Flächeninhalt des Dreiecks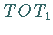 
zwischen der Tangente und beiden Asymptoten
beträgt für jeden Berührungspunkt
 |
(3.357) |
Der Flächeninhalt des Parallelogramms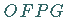 
,
das von den Asymptoten und zwei zu
ihnen vom Punkt
ausgehenden Parallelen gebildet wird, beträgt
 |
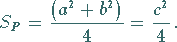(3.358) |
