Definitionen
Die affinen Koordinaten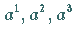 
eines Vektors 
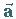in einem System mit den
Grundvektoren 
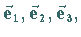definiert durch die Formel
 |
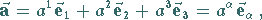(3.299) |
werden auch kontravariante Koordinaten dieses Vektors genannt.
Im Gegensatz dazu entsprechen seine kovarianten Koordinaten den Koeffizienten einer
Vektorzerlegung zu den Grundvektoren
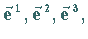d.h. zu den reziproken
Grundvektoren von 
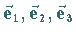(s. Lit. 22.18, Bd. 11).
Mit den kovarianten Koordinaten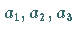 
des Vektors
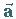ergibt sich
 |
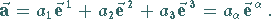(3.300) |
Im System der kartesischen Koordinaten stimmen die kovarianten Koordinaten eines Vektors
mit seinen kontravarianten Koordinaten überein.
