Kartesische Koordinaten
Gemäß (3.262a) kann jeder Vektor
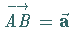 eindeutig in eine Summe von
Vektoren zerlegt werden, die parallel zu den Grundvektoren des Koordinatensystems
eindeutig in eine Summe von
Vektoren zerlegt werden, die parallel zu den Grundvektoren des Koordinatensystems
 stehen:
stehen:
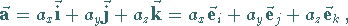 |
(3.263a) |
wobei die Skalare 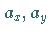 und
und 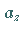 die kartesischen Koordinaten des
Vektors
die kartesischen Koordinaten des
Vektors 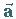 im System mit den Einheitsvektoren des Koordinatensystems
im System mit den Einheitsvektoren des Koordinatensystems
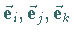 sind.
Man schreibt dafür auch
sind.
Man schreibt dafür auch
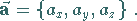 |
(3.263b) |
Die durch die drei Einheitsvektoren festgelegten Richtungen bilden ein senkrechtes
Richtungstripel .
Die kartesischen Koordinaten eines Vektors sind die Projektionen dieses Vektors
auf die Koordinatenachsen.
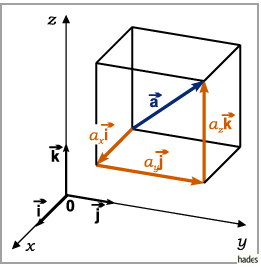
Wird ein Vektor parallel zu oder entlang einer der Koordinatenachsen verschoben, dann
ändern sich seine Koordinaten in den anderen beiden Richtungen nicht.
Die Koordinaten einer Linearkombination mehrerer Vektoren ergeben sich als
gleichgestaltete Linearkombination der Koordinaten dieser Vektoren, so daß
die Vektorgleichung (3.260b) drei skalaren Komponentengleichungen entspricht:
Für die Koordinaten der Summe und der Differenz zweier Vektoren
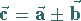 |
(3.265a) |
gilt insbesondere
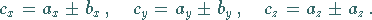 |
(3.265b) |
Der Radiusvektor  eines Punktes
eines Punktes 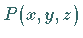 hat die kartesischen Koordinaten
dieses Punktes:
hat die kartesischen Koordinaten
dieses Punktes:
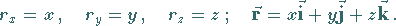 |
(3.266) |