Spezielle Vektoren
a) Einheitsvektor
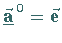wird ein Vektor
genannt, dessen Länge oder Absolutbetrag gleich 
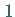ist.
Mit seiner Hilfe kann ein Vektor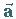 
durch das Produkt aus Einheitsvektor und
Modul gemäß
 |
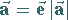(3.259a) |
angegeben werden.
Zur Beschreibung der drei Koordinatenachsen in Richtung wachsender Koordinatenwerte
werden oft die Einheitsvektoren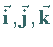 
oder
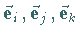verwendet.
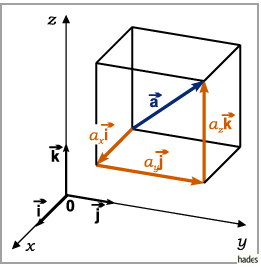
In der Abbildung bilden die durch die drei Einheitsvektoren festgelegten Richtungen
ein senkrechtes Richtungstripel .
Außerdem bilden sie ein orthogonales Koordinatensystem , denn es gilt:
 |
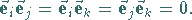(3.259b) |
Zudem gilt
 |
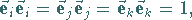(3.259c) |
so daß man von einem orthonormierten Koordinatensystem spricht.
b) Nullvektor heißt ein Vektor mit dem Absolutbetrag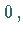 
also mit
zusammenfallendem Anfangs- und Endpunkt sowie mit unbestimmter Richtung im Raum.
c) Radiusvektor 
eines Punktes 
wird ein Vektor
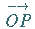genannt, dessen Anfangspunkt sich im
Koordinatenursprung befindet.
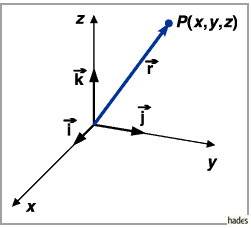
In diesem Falle heißt der Koordinatenursprung Pol .
Der Punkt
ist durch seinen Radiusvektor eindeutig bestimmt.
d) Kollineare Vektoren verlaufen parallel zu ein und derselben Geraden.
e) Komplanare Vektoren verlaufen parallel zu ein und derselben Ebene.
Für sie gilt das Spatprodukt
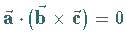(3.282).
