Schnittpunkte zweier Orthodromen
Die betrachteten Orthodromen sollen die nordpolnächsten Punkte
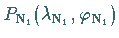und
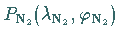besitzen, wobei
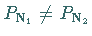gilt.
Einsetzen des Schnittpunktes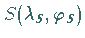 
in beide Orthodromengleichungen
führt auf das Gleichungssystem
 |
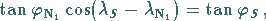(3.252a) |
 |
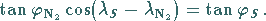(3.252b) |
Elimination von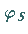 
und die Anwendung der Additionstheoreme auf die
Kosinusfunktionen ergeben:
 |
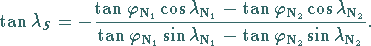(3.253) |
Diese Gleichung liefert im Definitionsbereich
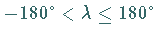der geographischen Längen zwei Lösungen
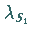und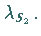 
Die dazugehörigen geographischen Breiten ergeben sich aus (3.252a):
 |
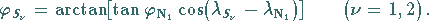(3.254) |
Die Schnittpunkte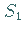 
und 
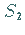sind Gegenpunkte , d.h., sie gehen durch eine
Spiegelung am Kugelmittelpunkt auseinander hervor.
