Gleichung der Loxodrome

Die Abbildung zeigt eine Loxodrome mit dem Kurswinkel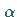

durch den laufenden Punkt

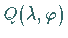und den infinitesimal benachbarten Punkt

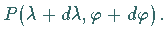
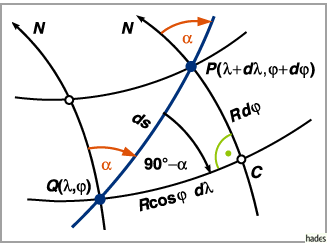
Das rechtwinklige sphärische Dreieck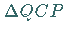

kann wegen seiner differentiellen Ausmaße als ebenes Dreieck angesehen werden. Dann gilt:

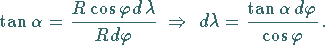(3.245a)

Unter Berücksichtigung des Umstandes, daß die Loxodrome durch den Punkt

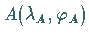verlaufen soll, ergibt sich daraus durch Integration die Gleichung der Loxodrome:

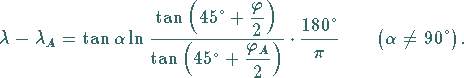(3.245b)

Ist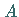

speziell der Schnittpunkt

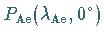der Loxodrome mit dem Äquator, so folgt daraus:

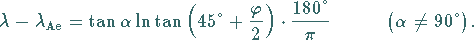(3.245c)

Hinweis: Die Berechnung vo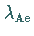n kann mit (3.250) erfolgen.