Geometrische Definition der Hyperbelfunktionen
In Analogie zur Definition der trigonometrischen Funktionen mit Hilfe der
Kreissektorfläche (s. (3.3), (3.4),
(3.5)) wird anstelle der Sektorfläche des Kreises mit der
Gleichung 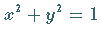 die entsprechende Sektorfläche der Hyperbel mit der
Gleichung
die entsprechende Sektorfläche der Hyperbel mit der
Gleichung 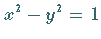 (rechte Abbildung) betrachtet.
(rechte Abbildung) betrachtet.
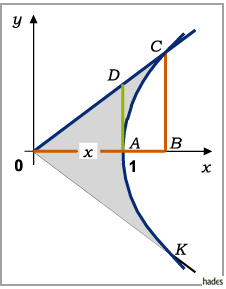
Mit der Bezeichnung 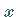 für diese Fläche
für diese Fläche  (schattiert gezeichnet), lauten die
Definitionsgleichungen der Hyperbelfunktionen:
(schattiert gezeichnet), lauten die
Definitionsgleichungen der Hyperbelfunktionen:
 |
(3.9) |
 |
(3.10) |
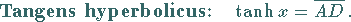 |
(3.11) |
Berechnung der Fläche 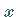 durch Integration und Ausdrücken des Ergebnisses mit
durch Integration und Ausdrücken des Ergebnisses mit
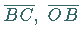 und
und 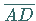 liefert
liefert
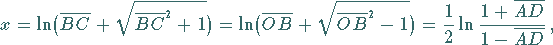 |
(3.12) |
so daß die Hyperbelfunktionen nunmehr mit Hilfe von Exponentialfunktionen darstellbar
sind:
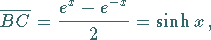 |
(3.13) |
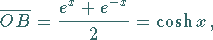 |
(3.14) |
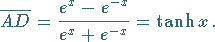 |
(3.15) |
Das sind die Definitionsgleichungen der Hyperbelfunktionen.
Die Bezeichnung Hyperbelfunktionen ist offenkundig.
![]() durch Integration und Ausdrücken des Ergebnisses mit
durch Integration und Ausdrücken des Ergebnisses mit
![]() und
und ![]() liefert
liefert