Schnittpunkte mit einem Breitenkreis
Für die Schnittpunkte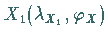 
und
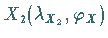einer Orthodrome mit dem Breitenkreis
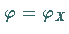ergibt sich gemäß (3.229):
 |
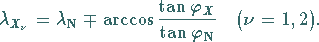(3.235) |
Nach der NEPERschen Regel gilt für die beiden Schnittwinkel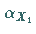 
und
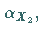unter denen eine Orthodrome mit dem nordpolnächsten Punkt
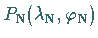den Breitenkreis
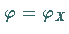schneidet:
 |
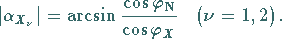(3.236) |
Für den minimalen Kurswinkel 
muß das Argument in der
Arkussinusfunktion hinsichtlich der Variablen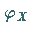 
extremal sein.
Man erhält: 
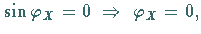d.h., in den Schnittpunkten
mit dem Äquator ist der Betrag des Kurswinkels minimal:
 |
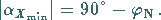(3.237) |
Hinweis 1: Lösungen von (3.235) ergeben sich nur für
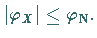
Hinweis 2: Unter Umständen ist gemäß (3.230) eine
Rückversetzung der Winkel erforderlich.
