Gleichung der Orthodrome
Bewegungen auf Orthodromen - die Meridiane und der Äquator ausgenommen - sind mit der
Notwendigkeit einer ständigen Kursänderung verbunden.
Solche Orthodromen mit ortsabhängigen Kurswinkeln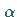 
können eindeutig unter
Zuhilfenahme ihres nordpolnächsten Punktes
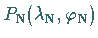beschrieben werden, wobei 
ist.
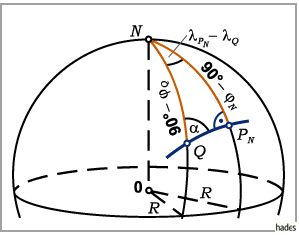
Im nordpolnächsten Punkt hat die Orthodrome den Kurswinkel
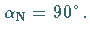Die Gleichung der Orthodrome durch 
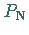und den laufenden Punkt
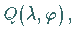dessen relative Lage zu
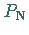beliebig ist, ergibt sich
nach der NEPERschen Regel gemäß als:
 |
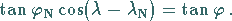(3.229) |
