|
|
|
|
| Beispiel A | |
|
Es ist die kürzeste Entfernung zwischen Dresden
Lösung: Die geographischen Koordinaten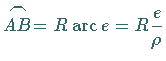 
und der Nordpol 
liefern zwei auf
Meridianen liegende Seiten 
und 
des Dreiecks 
sowie den eingeschlossenen Winkel
Für 
folgt aus dem Kosinussatz
(3.191a)
also  .
Der Großkreisabschnitt 
hat gemäß
(3.179a)
die Länge  .
| |
| Beispiel B | |
|
Es sind die Kurswinkel Lösung: Die Berechnung der zwei Seiten 
sowie des eingeschlossenen Winkels
im sphärischen Dreieck
mit
den geographischen Koordinaten
mit Hilfe des Kosinussatzes
(3.191c)
liefert
 ,
und wegen 
ergibt sich
 .
Mit dem Seitenkosinussatz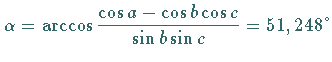
(3.191a)
erhält man
und
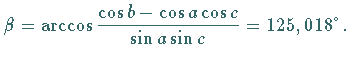
Somit ist | |
Hinweis: Die Verwendung des Sinussatzes zur Berechnung von Seiten und Winkeln ist nur dann sinnvoll, wenn aus der Aufgabenstellung ersichtlich ist, ob diese spitz oder stumpf sind.
|
|
und Alma Ata
zu berechnen.
und 
bei Abfahrt
und Ankunft sowie die Entfernung in Seemeilen für eine Schiffsreise auf einem
Großkreis von Bombay
nach Dar es Saalam
zu berechnen.
und
.