Die Eckpunkte 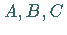 des sphärischen Dreiecks teilen jeden Großkreis durch zwei
Eckpunkte im allgemeinen in zwei ungleiche Teile.
Dadurch entstehen mehrere verschiedene sphärische Dreiecke, z.B. auch das sphärische
Dreieck mit den Seiten
des sphärischen Dreiecks teilen jeden Großkreis durch zwei
Eckpunkte im allgemeinen in zwei ungleiche Teile.
Dadurch entstehen mehrere verschiedene sphärische Dreiecke, z.B. auch das sphärische
Dreieck mit den Seiten 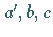 und der in der folgenden linken Abbildung schattierten
Fläche.
und der in der folgenden linken Abbildung schattierten
Fläche.
Gemäß einer Festsetzung von EULER werden für die Seiten des sphärischen
Dreiecks nur die Großkreisbogen gewählt, die kleiner als 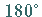 sind.
Das entspricht der Definition der Seiten als sphärische Abstände zwischen den
Dreieckspunkten.
In diesem Zusammenhang bezeichnet man sphärische Dreiecke, bei denen jede Seite und
jeder Winkel kleiner als
sind.
Das entspricht der Definition der Seiten als sphärische Abstände zwischen den
Dreieckspunkten.
In diesem Zusammenhang bezeichnet man sphärische Dreiecke, bei denen jede Seite und
jeder Winkel kleiner als 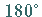 ist, als EULERsche Dreiecke, anderenfalls
als Nicht- EULERsche Dreiecke.
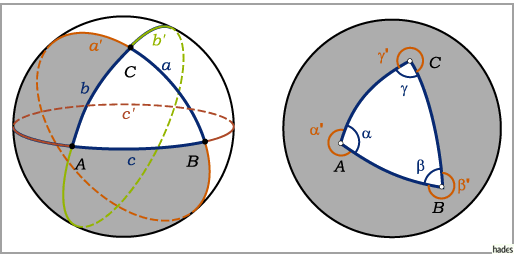
Die rechte Abbildung zeigt ein EULERsches und ein Nicht- EULERsches
Dreieck.
ist, als EULERsche Dreiecke, anderenfalls
als Nicht- EULERsche Dreiecke.
Die rechte Abbildung zeigt ein EULERsches und ein Nicht- EULERsches
Dreieck.