Sphärisches Zweieck
Durch die Endpunkte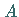 
und 
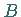eines Kugeldurchmessers sollen zwei Ebenen 
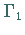und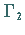 
verlaufen, die den Winkel 
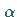miteinander einschließen und zwei
Großkreishälften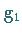 
und 
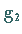definieren.
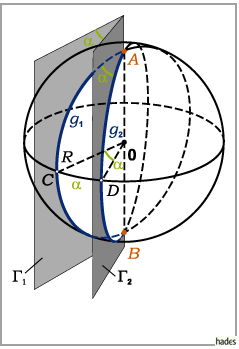
Der von zwei Großkreishälften begrenzte Teil der Kugeloberfläche wird
sphärisches Zweieck oder Kugelzweieck genannt.
Als Seiten des sphärischen Zweiecks werden die sphärischen Abstände zwischen den
Punkten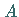
und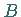
auf den Großkreisen definiert.
Jede Seite beträgt daher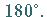 
Als Winkel des sphärischen Zweiecks werden die Winkel zwischen den Tangenten an die
Großkreise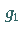 
und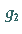 
in den Punkten
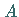und
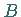definiert.
Sie sind gleich und stimmen mit dem sogenannten Keilwinkel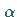
zwischen den
Ebenen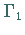
und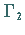
überein.
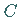Sind 
und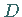 
die Halbierungspunkte der beiden Großkreisbogen durch
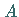und ,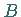
dann kann der Winkel
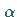auch als sphärischer Abstand der Punkte
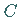und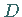
aufgefaßt werden.
Die Fläche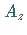 
des Kugelzweiecks verhält sich zur Kugelfläche wie der Winkel
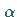zu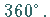 
Daraus folgt
 |
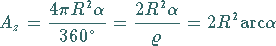(3.182) |
mit Umrechnungsfaktor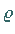 
gemäß (3.179c).
