Differentialoperatoren
Der Operator der Differentiation lautet in Maple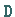 
.
Seine Anwendung erfolgt auf Funktionen in Operatorform entsprechend 
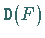bzw.
.
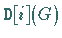Im ersten Fall wird die Ableitung einer Funktion von einer Variablen in Operatorform
bestimmt.
Das Anhängen der geklammerten Variablen ergibt die Ableitung als Funktion.
In anderer Form läßt sich dies als 
schreiben.
Höhere Ableitungen erhält man durch Mehrfachanwendung des Operators ,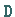
was sich vereinfacht als
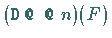schreiben läßt, wobei
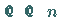die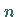 
-te
,,Potenz`` des Differentialoperators bedeutet.
Ist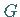 
eine Funktion mehrerer Variabler, so erzeugt
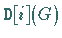die partielle
Ableitung von
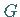nach der 
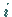-ten Variablen.
Auch dieses Ergebnis ist wieder ein Operator.
Mit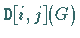 
erhält man 
,
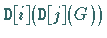d.h. die zweite partielle
Ableitung nach der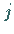 
-ten und 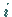-ten Variablen.
Entsprechend kann man höhere Ableitungen bilden.
Für den Diffentialoperator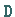
gelten die aus der
Differentialrechnung bekannten Grundregeln, wobei 
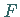und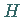 
differenzierbare Funktionen sind.
 |
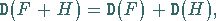(20.48a) |
 |
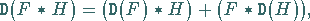(20.48b) |
 |
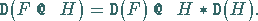(20.48c) |
