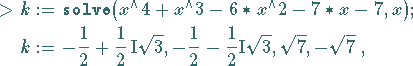Wichtige Operationen
Die beiden grundsätzlichen Operationen zur symbolischen Lösung von Gleichungen in
Maple sind 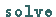 und
und 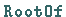 bzw.
bzw.  .
Mit ihnen und ihren möglichen Variationen durch bestimmte optionale Argumente gelingt
es, eine Vielzahl von Gleichungen, auch transzendente, zu lösen.
Wenn eine Gleichung nicht in geschlossener Form lösbar ist, kann Maple nur
numerische Näherungslösungen anbieten.
.
Mit ihnen und ihren möglichen Variationen durch bestimmte optionale Argumente gelingt
es, eine Vielzahl von Gleichungen, auch transzendente, zu lösen.
Wenn eine Gleichung nicht in geschlossener Form lösbar ist, kann Maple nur
numerische Näherungslösungen anbieten.
Die Funktion 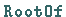 ist das Symbol für alle Wurzeln einer Gleichung einer
Variablen.
Mit
ist das Symbol für alle Wurzeln einer Gleichung einer
Variablen.
Mit
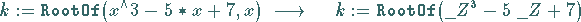 |
(20.58) |
versteht Maple unter 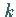 die Gesamtheit der Wurzeln der Gleichung
die Gesamtheit der Wurzeln der Gleichung 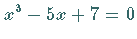 .
Dabei wird der eingegebene Ausdruck, wenn möglich, in eine einfache Form gebracht und
mit der globalen Variablen
.
Dabei wird der eingegebene Ausdruck, wenn möglich, in eine einfache Form gebracht und
mit der globalen Variablen 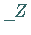 dargestellt.
Der Aufruf
dargestellt.
Der Aufruf  liefert eine Folge der Wurzeln.
liefert eine Folge der Wurzeln.
Der Befehl 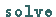 liefert die Lösung einer Gleichung, sofern diese
existiert.
liefert die Lösung einer Gleichung, sofern diese
existiert.
| Beispiel |
|
während
ergibt.
Diese Gleichung besitzt im Bereich der rationalen Zahlen keine Lösungen.
Mit 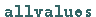 erhält man genäherte numerische Lösungen.
erhält man genäherte numerische Lösungen.
|
![]() ist das Symbol für alle Wurzeln einer Gleichung einer
Variablen.
Mit
ist das Symbol für alle Wurzeln einer Gleichung einer
Variablen.
Mit
![]() liefert die Lösung einer Gleichung, sofern diese
existiert.
liefert die Lösung einer Gleichung, sofern diese
existiert.