Potenzfunktion
Die Potenzfunktion
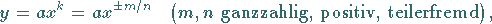 |
(2.53) |
ist für 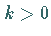 und
und 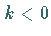 getrennt zu betrachten.
Dabei reicht eine Beschränkung auf den Fall
getrennt zu betrachten.
Dabei reicht eine Beschränkung auf den Fall  aus, weil die Kurven für
aus, weil die Kurven für
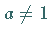 gegenüber der von
gegenüber der von 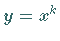 in Richtung der
in Richtung der 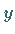 -Achse mit dem Faktor
-Achse mit dem Faktor
 gestreckt und bei negativem
gestreckt und bei negativem  an der
an der  -Achse zu spiegeln sind.
-Achse zu spiegeln sind.
a) Fall
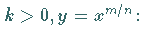 Der Kurvenverlauf ist für vier charakteristische Fälle der Größen
Der Kurvenverlauf ist für vier charakteristische Fälle der Größen 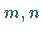 in den folgenden Abbildungen dagestellt.
in den folgenden Abbildungen dagestellt.
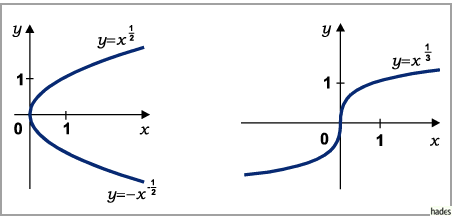
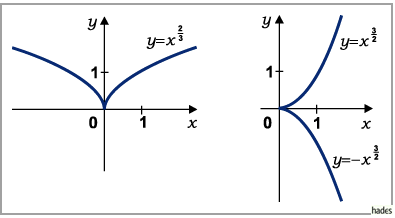
Die Kurve verläuft durch die Punkte (0,0) und (1,1).
Für 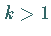 berührt sie die
berührt sie die  -Achse im Koordinatenursprung (s. 4. Abbildung), für
-Achse im Koordinatenursprung (s. 4. Abbildung), für
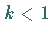 ebenfalls im Koordinatenursprung die
ebenfalls im Koordinatenursprung die 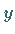 -Achse (s. 1. bis 3. Abbildung).
Für
-Achse (s. 1. bis 3. Abbildung).
Für 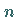 gerade gibt es zwei zur
gerade gibt es zwei zur  -Achse
symmetrische Zweige (1. und 4. Abbildung), für
-Achse
symmetrische Zweige (1. und 4. Abbildung), für 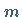 gerade zwei zur
gerade zwei zur 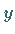 -Achse
symmetrische Zweige (2. und 3. Abbildung).
Für
-Achse
symmetrische Zweige (2. und 3. Abbildung).
Für 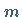 und
und 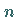 ungerade ist die Kurve zentralsymmetrisch zum Koordinatenursprung
(2. Abbildung).
Die Kurve kann somit im Koordinatenursprung einen Scheitel, einen Wendepunkt oder einen
Rückkehrpunkt besitzen. Asymptoten hat sie keine.
ungerade ist die Kurve zentralsymmetrisch zum Koordinatenursprung
(2. Abbildung).
Die Kurve kann somit im Koordinatenursprung einen Scheitel, einen Wendepunkt oder einen
Rückkehrpunkt besitzen. Asymptoten hat sie keine.
b) Fall
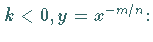 Der Kurvenverlauf ist für drei charakteristische Fälle der Größen
Der Kurvenverlauf ist für drei charakteristische Fälle der Größen 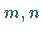 in den folgenden Abbildungen dagestellt.
in den folgenden Abbildungen dagestellt.
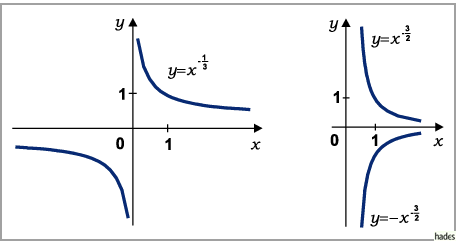
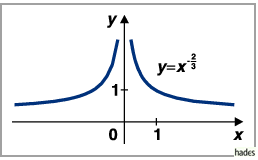
Die Kurve ist vom hyperbolischen Typ, wobei die Asymptoten mit den Koordinatenachsen
zusammenfallen. Die Unstetigkeitsstelle befindet sich bei 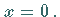 Die Kurve nähert sich der
Die Kurve nähert sich der  -Achse asymptotisch um so schneller und der
-Achse asymptotisch um so schneller und der
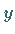 -Achse um so langsamer, je größer
-Achse um so langsamer, je größer 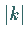 ist.
Der Kurvenverlauf und die Symmetrie hinsichtlich der Koordinatenachsen bzw. des
Koordinatenursprungs hängen wie im Falle
ist.
Der Kurvenverlauf und die Symmetrie hinsichtlich der Koordinatenachsen bzw. des
Koordinatenursprungs hängen wie im Falle 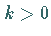 davon ab, ob
davon ab, ob 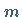 und
und 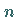 gerade oder
ungerade sind. Extrema gibt es keine.
gerade oder
ungerade sind. Extrema gibt es keine.