Parabel n-ter Ordnung
Die Funktion
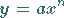 |
(2.44) |
mit 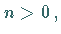 ganzzahlig, liefert als Kurve eine Parabel
ganzzahlig, liefert als Kurve eine Parabel 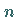 -ter Ordnung .
-ter Ordnung .
Spezialfall
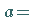
 :
Die Kurve
:
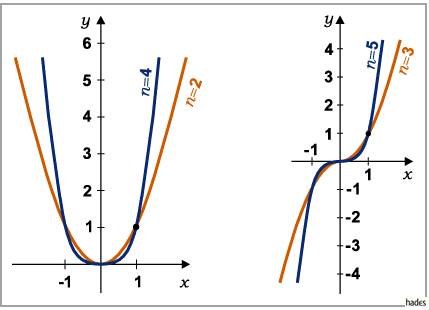
Die Kurve 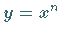 geht durch die Punkte (0,0) und (1,1) und berührt oder schneidet
die
geht durch die Punkte (0,0) und (1,1) und berührt oder schneidet
die  -Achse im Koordinatenursprung.
Für gerades
-Achse im Koordinatenursprung.
Für gerades 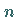 ergibt sich eine zur
ergibt sich eine zur 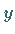 -Achse symmetrische Kurve mit einem Minimum
im Koordinatenursprung.
Für ungerades
-Achse symmetrische Kurve mit einem Minimum
im Koordinatenursprung.
Für ungerades 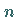 ergibt sich eine zentralsymmetrische Kurve zum Koordinatenursprung,
der zugleich Wendepunkt ist. Asymptoten gibt es keine.
ergibt sich eine zentralsymmetrische Kurve zum Koordinatenursprung,
der zugleich Wendepunkt ist. Asymptoten gibt es keine.
Allgemeiner Fall

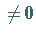 :
Man erhält die Kurve
:
Man erhält die Kurve 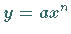 aus der zu
aus der zu 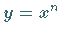 gehörenden Kurve durch
Streckung der Abszissen mit dem Faktor
gehörenden Kurve durch
Streckung der Abszissen mit dem Faktor 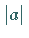 .
Für
.
Für 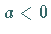 spiegelt man
spiegelt man 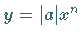 an der
an der  -Achse.
-Achse.