|
Die reduzierte Gleichung 3. Grades 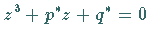 ist von der Form (2.292b).
Setzt man
ist von der Form (2.292b).
Setzt man 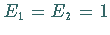 und
und 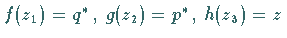 ,
so
lauten die Formeln für die Berechnung der Koordinaten der Kurvenskala ,
so
lauten die Formeln für die Berechnung der Koordinaten der Kurvenskala
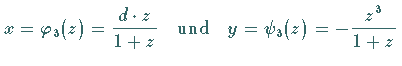 . .
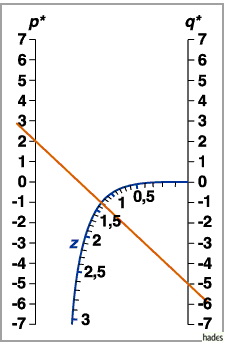
In der folgenden Abbildung ist die Kurvenskala nur für positive 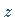 -Werte
gezeichnet worden. -Werte
gezeichnet worden.
Die negativen Wurzeln erhält man, wenn man 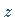 durch
durch 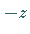 ersetzt und dann
die positiven Wurzeln der Gleichung
ersetzt und dann
die positiven Wurzeln der Gleichung 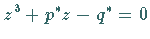 bestimmt.
bestimmt.
Auch die komplexen Wurzeln 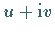 lassen sich aus dem
Nomogramm bestimmen.
Bezeichnet man die stets existierende reelle Wurzel mit
lassen sich aus dem
Nomogramm bestimmen.
Bezeichnet man die stets existierende reelle Wurzel mit 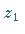 ,
dann ist der
Realteil der komplexen Wurzel ,
dann ist der
Realteil der komplexen Wurzel 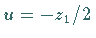 ,
und der Imaginärteil ,
und der Imaginärteil 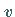 kann aus
der Gleichung
kann aus
der Gleichung 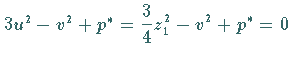 ermittelt
werden.
ermittelt
werden.
Ablesebeispiel: 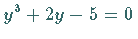 ,
d.h. ,
d.h. 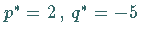 .
Man liest .
Man liest 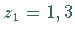 ab.
ab.
| 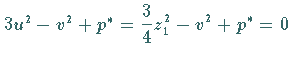 ermittelt
werden.
ermittelt
werden.