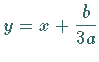1. Normalform:
 |
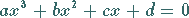(1.155a) |
oder nach Division durch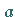 
und Substitution von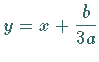 
 |
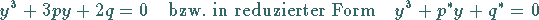(1.155b) |
mit
 |
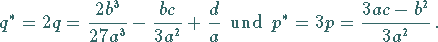(1.155c) |
2. Anzahl der Lösungen: In Abhängigkeit vom Vorzeichen der Diskriminante
 |
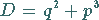(1.156) |
ergibt sich:
- für
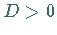eine reelle Lösung (eine reelle und zwei komplexe Wurzeln),
- für
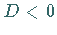drei reelle Lösungen (drei verschiedene reelle Wurzeln),
- für
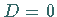eine reelle Lösung (eine dreifache reelle Wurzel) im Falle
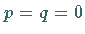oder zwei reelle Lösungen (eine einfache reelle Wurzel und eine zweifache
reelle Wurzel) im Falle 
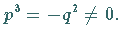
3. Eigenschaften der Wurzeln der kubischen Gleichung: Sind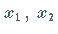 
und 
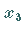die Wurzeln der kubischen Gleichung (1.155a),
dann gilt:
 |
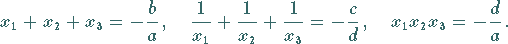(1.157) |
Hinweis: Zur Lösung der Gleichung 3. Grades werden in den nächsten drei
Abschnitten drei Methoden betrachtet.
Eine vierte Lösungsmethode beruht auf Näherungsverfahren.
