Einfach-logarithmisches Funktionspapier
Ist die  -Achse gleichabständig unterteilt, die
-Achse gleichabständig unterteilt, die 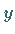 -Achse jedoch logarithmisch,
dann spricht man vom einfach-logarithmischen Funktionspapier oder vom
einfach-logarithmischen Koordinatensystem .
-Achse jedoch logarithmisch,
dann spricht man vom einfach-logarithmischen Funktionspapier oder vom
einfach-logarithmischen Koordinatensystem .
Skalengleichungen:
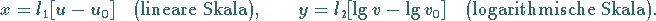 |
(2.259) |
Die folgende Abbildung zeigt ein Beispiel für einfach-logarithmisches Papier.
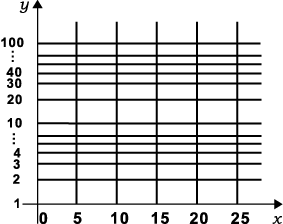
Darstellung von Exponentialfunktionen: Auf einfach-logarithmischem Papier
werden Exponentialfunktionen der Form
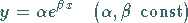 |
(2.260) |
als Geraden dargestellt (s. Rektifizierung).
Diese Eigenschaft wird wie folgt ausgenutzt: Liegen Meßpunkte, wenn sie in
einfach-logarithmischem Papier eingetragen worden sind, annähernd auf einer Geraden,
dann kann zwischen den Variablen ein Zusammenhang der Form (2.260)
angenommen werden.
Mit Hilfe dieser Geraden, die nach Augenmaß durch die Meßpunkte gelegt wird, kann
man Näherungswerte für die Parameter 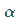 und
und 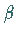 bestimmen:
bestimmen:
Liest man zwei Punkte 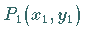 und
und 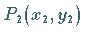 auf dieser Geraden ab, dann
erhält man
auf dieser Geraden ab, dann
erhält man
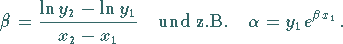 |
(2.261) |