Schleppkurve oder Traktrix
Schleppkurve oder Traktrix nennt man den geometrischen Ort
aller Punkte mit der Eigenschaft, daß das Tangentenstück 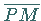 einer Kurve zwischen Berührungspunkt
einer Kurve zwischen Berührungspunkt 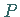 und Schnittpunkt der Tangente mit einer
Leitlinie, hier mit der
und Schnittpunkt der Tangente mit einer
Leitlinie, hier mit der  -Achse, die konstante Länge
-Achse, die konstante Länge  besitzt.
besitzt.
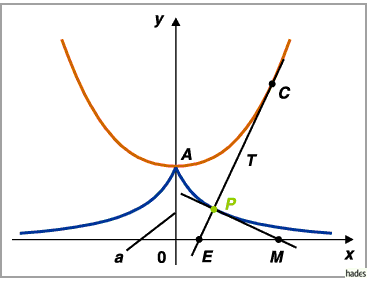
In der Abbildung ist die Traktrix blau gezeichnet.
Die Traktrix wird von einem Punkt 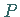 ,
Schleppunkt genannt, beschrieben,
der an einem Ende eines nicht dehnbaren Fadens mit der Länge
,
Schleppunkt genannt, beschrieben,
der an einem Ende eines nicht dehnbaren Fadens mit der Länge  befestigt ist,
wenn das andere Ende
befestigt ist,
wenn das andere Ende 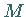 entlang der Leitlinie, hier entlang der
entlang der Leitlinie, hier entlang der  -Achse, bewegt
wird.
-Achse, bewegt
wird.
Die Gleichung der Traktrix lautet
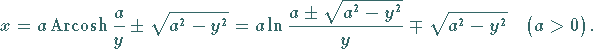 |
(2.242) |
Die  -Achse ist Asymptote. Der Punkt
-Achse ist Asymptote. Der Punkt 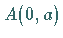 ist eine Spitze.
Die Kurve verläuft symmetrisch zur
ist eine Spitze.
Die Kurve verläuft symmetrisch zur 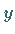 -Achse.
-Achse.
Die Länge des Bogens 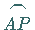 ist
ist 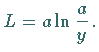 Bei wachsender Länge des Bogens
Bei wachsender Länge des Bogens 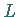 nähert sich die Differenz
nähert sich die Differenz
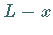 dem Wert
dem Wert 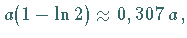 wobei
wobei  hier die Abszisse des Punktes
hier die Abszisse des Punktes
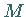 ist.
ist.
Der Krümmungsradius ist 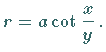 Krümmungsradius
Krümmungsradius 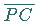 und Normalenabschnitt
und Normalenabschnitt 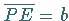 sind
zueinander umgekehrt proportional:
sind
zueinander umgekehrt proportional: 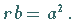
Die Evolute der Traktrix, d.h., der geometrische Ort ihrer
Krümmungskreismittelpunkte 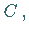 in der Abbildung rot dargestellt, ist die
Katenoide mit der Gleichung
in der Abbildung rot dargestellt, ist die
Katenoide mit der Gleichung
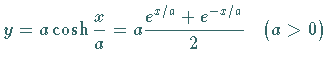 (2.241).
(2.241).
![]() -Achse ist Asymptote. Der Punkt
-Achse ist Asymptote. Der Punkt ![]() ist eine Spitze.
Die Kurve verläuft symmetrisch zur
ist eine Spitze.
Die Kurve verläuft symmetrisch zur ![]() -Achse.
-Achse.
![]() ist
ist 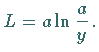 Bei wachsender Länge des Bogens
Bei wachsender Länge des Bogens ![]() nähert sich die Differenz
nähert sich die Differenz
![]() dem Wert
dem Wert ![]() wobei
wobei ![]() hier die Abszisse des Punktes
hier die Abszisse des Punktes
![]() ist.
ist.
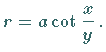 Krümmungsradius
Krümmungsradius ![]() und Normalenabschnitt
und Normalenabschnitt ![]() sind
zueinander umgekehrt proportional:
sind
zueinander umgekehrt proportional: ![]()
![]() in der Abbildung rot dargestellt, ist die
Katenoide mit der Gleichung
in der Abbildung rot dargestellt, ist die
Katenoide mit der Gleichung
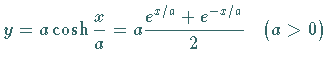 (2.241).
(2.241).