|
|
|
|
 |
(2.240a) |
 |
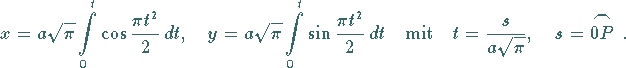(2.240b) |
Die Integrale können nicht durch elementare Funktionen ausgedrückt werden; sie lassen
sich aber für jeden Parameter 
durch
numerische Integration berechnen, so daß die Klotoide punktweise
gezeichnet werden kann.
Wegen der Berechnung am Computer s. Lit. 3.12.
Die Kurve ist zentralsymmetrisch zum Koordinatenursprung, der gleichzeitig Wendepunkt ist.
Im Wendepunkt ist die 
-Achse Tangente. Bei 
und 
hat die Kurve je einen
asymptotischen Punkt mit den Koordinaten
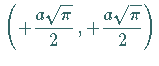bzw.
.
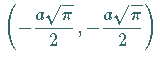Die Klotoide findet z.B. beim Straßenbau Anwendung, wo der Übergang von einer Geraden in eine Kreiskurve durch einen Klotoidenabschnitt vermittelt wird (s. Lit. 3.12).
|
|