Hypozykloide und Astroide
Hypozykloide wird eine Kurve genannt, die von einem Peripheriepunkt eines
Kreises beschrieben wird, wenn dieser, ohne zu gleiten, auf der Innenseite eines
anderen Kreises abrollt.
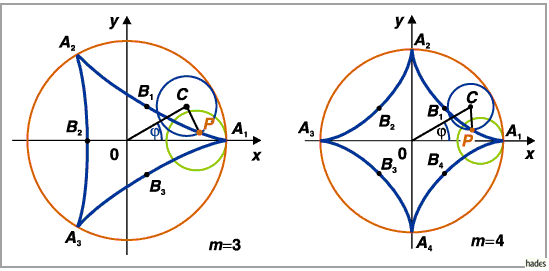
Die Gleichung der Hypozykloide, die Koordinaten der Scheitelpunkte und Spitzen,
die Formeln für die Bogenlängen, die Flächeninhalte und die Krümmungsradien
entsprechen denen der Epizykloide, es ist jedoch ,,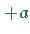
`` durch ,,
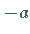`` zu ersetzen.
Die Anzahl der Spitzen entspricht für 
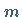ganzzahlig, rational oder
irrational (stets ist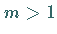 
)
der von der Epizykloide bekannten.
Fall
Für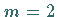 
entartet die Kurve in den Durchmesser des unbeweglichen Kreises.
Fall
Für 
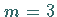besitzt die Hypozykloide drei Zweige mit der Gleichung
 |
(2.234a) |
Es gilt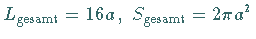 
.
Fall
Für 
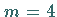besitzt die Hypozykloide vier Zweige und wird Astroide genannt.
Ihre Gleichung lautet in kartesischen Koordinaten und in Parameterform:
 |
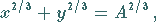(2.234b) |
 |
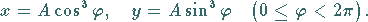(2.234c) |
Es gilt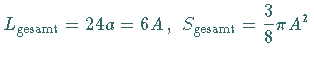 
.
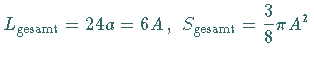