Relaxationsverfahren
Die Iterationsvorschrift des GAUSS-SEIDEL-Verfahrens (19.51)
läßt sich auch in der sogenannten Korrekturform
schreiben.
Durch geeignete Wahl eines Relaxationsparameters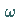 
,
so daß
(19.52) in
 |
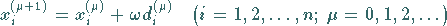(19.53) |
übergeht, kann man versuchen, die Konvergenzeigenschaften des Einzelschrittverfahrens
zu verbessern.
Es läßt sich zeigen, daß Konvergenz nur für
 |
(19.54) |
möglich ist.
Für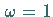 
erhält man das Einzelschrittverfahren.
Im Fall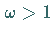 
spricht man von Überrelaxation, die zugehörigen
Iterationsverfahren werden als SOR-Verfahren (successive
over relaxation) bezeichnet.
Die Bestimmung optimaler Relaxationsparameter ist nur für einige spezielle Matrizentypen
explizit möglich.
Die Anwendung iterativer Methoden zur Lösung linearer Gleichungssysteme ist vor allem
angebracht, wenn die Hauptdiagonalelemente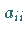 
der Koeffizientenmatrix gegenüber
den übrigen Elementen 
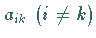betragsmäßig stark überwiegen
oder wenn durch Umstellung oder geeignete Kombination der einzelnen Gleichungen eine
solche Anordnung erreicht werden kann.
