Prinzip der B-B-Kurvendarstellung
Gegeben seien 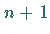 Eckpunkte
Eckpunkte 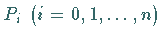 mit den Ortsvektoren
mit den Ortsvektoren
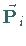 eines räumlichen Polygons, das in diesem Zusammenhang als
Stützpolygon bezeichnet wird.
Durch die Vorschrift
eines räumlichen Polygons, das in diesem Zusammenhang als
Stützpolygon bezeichnet wird.
Durch die Vorschrift
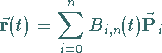 |
(19.252) |
wird diesen Punkten eine Raumkurve, die sogenannte B-B-Kurve zugeordnet.
Wegen (19.249) kann (19.252) als ,,variable Konvexkombination`` der gegebenen Punkte aufgefaßt werden.
Die Raumkurve (19.252) hat folgende wichtige Eigenschaften:
1. Die Punkte 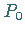 und
und 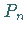 werden interpoliert.
werden interpoliert.
2. Die Vektoren 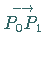 und
und
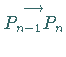 sind Tangenten von
sind Tangenten von
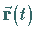 in
in 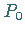 bzw.
bzw. 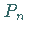 .
.
Den Zusammenhang zwischen Stützpolygon und B-B-Kurve zeigt die folgende Abbildung.
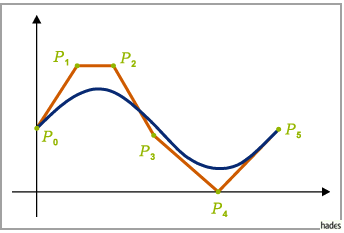
Die B-B-Darstellung wird vor allem für den Entwurf von Kurven eingesetzt, da man durch
die Änderung von Polygonecken den Kurvenverlauf auf sehr einfache Weise beeinflussen
kann.
Häufig werden an Stelle der BERNSTEINschen Grundpolynome normalisierte B-Splines
verwendet.
Die zugehörigen Raumkurven heißen dann B-Spline-Kurven.
Ihr Verlauf entspricht prinzipiell dem der B-B-Kurven, aber sie haben folgende Vorteile
gegenüber diesen:
1. Das Stützpolygon wird besser approximiert.
2. Bei Änderung von Polygoneckpunkten ändert sich die B-Spline-Kurve nur lokal.
3. Neben der lokalen Änderung des Kurvenverlaufs kann auch die Differenzierbarkeit
beeinflußt werden.
So lassen sich z.B. auch Knicke und Geradenstücke erzeugen.
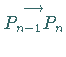 sind Tangenten von
sind Tangenten von