Eigenschaften
Der bikubische Interpolationsspline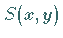 
ist durch folgende Eigenschaften eindeutig
festgelegt:
1.
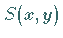erfüllt die Interpolationsbedingung
 |
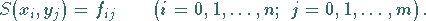(19.241) |
2. Auf jeder Masche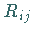 
des Rechteckbereiches 
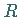ist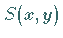
identisch mit
einem bikubischen Polynom, d.h., es gilt die Darstellung
 |
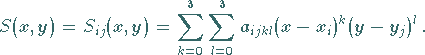(19.242) |
Damit wird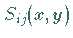 
durch 16 Ansatzkoeffizienten repräsentiert, und für
die Beschreibung von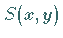
sind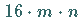 
Koeffizienten notwendig.
3. Die Ableitungen
 |
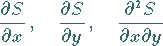(19.243) |
sind stetig auf .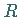
Damit wird eine gewisse Glattheit der gesuchten Fläche gewährleistet.
4.
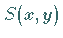erfüllt spezielle Randbedingungen:
Dabei si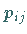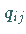nd 
,
und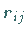 
vorgegebene Zahlenwerte.
Bei der Bestimmung der Ansatzkoeffizienten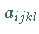 
können die Ergebnisse der
eindimensionalen kubischen Spline-Interpolation ganz entscheidend ausgenutzt werden.
Es zeigt sich:
1. Es ist eine sehr große Anzahl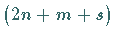 
linearer Gleichungssyteme, aber nur
mit tridiagonaler Koeffizientenmatrix, zu lösen.
2. Die linearen Gleichungssysteme unterscheiden sich im wesentlichen nur durch ihre
rechten Seiten.
Man kann im allgemeinen sagen, bikubische Interpolationssplines sind günstig
bzgl. Rechenzeit und Genauigkeit und damit recht gut geeignet für viele
praktische Anwendungen. Zur rechentechnischen Realisierung der
Koeffizientenbestimmung s. Lit. 19.6, 19.28.
