Die verschiedenen Verfahren unterscheiden sich in der Wahl der trennenden Hyperebenen
.
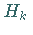Beim Verfahren von KELLEY wird 
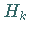auf folgende Weise bestimmt: Es wird 
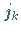derart gewählt, daß gilt
 |
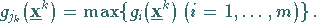(18.112) |
Die Funktion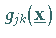 
besitzt im Punkt 
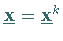die
Tangentialebene
 |
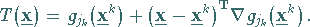(18.113) |
Die Hyperebene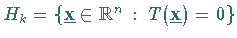 
trennt den Punkt
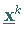von den Punkten 
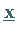mit 
.
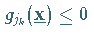Daher wird als weitere Restriktion für das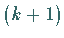 
-te lineare Programm
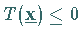gesetzt.
Jeder Häufungspunkt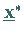 
der Folge 
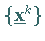ist ein Minimalpunkt des
Ausgangsproblems.
In der praktischen Rechnung zeigt das Verfahren eine geringe Konvergenzgeschwindigkeit.
Außerdem steigt die Restriktionszahl ständig an.
