Es wird das Optimierungsproblem
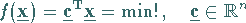 |
(18.106) |
über dem beschränkten Bereich 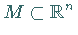 ,
der mit konvexen Funktionen
,
der mit konvexen Funktionen
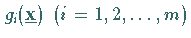 durch
durch 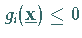 beschrieben
ist, betrachtet.
Ein Problem mit nichtlinearer, aber konvexer Zielfunktion
beschrieben
ist, betrachtet.
Ein Problem mit nichtlinearer, aber konvexer Zielfunktion 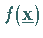 wird in diese Form
überführt, indem
wird in diese Form
überführt, indem
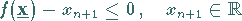 |
(18.107) |
als weitere Nebenbedingung aufgenommen und
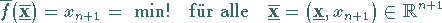 |
(18.108) |
mit 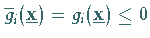 gelöst wird.
gelöst wird.
Die Grundidee des Verfahrens besteht in der iterativen linearen Approximation von 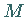 in
der Nähe des Minimalpunktes
in
der Nähe des Minimalpunktes 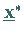 durch konvexe Polyeder, womit das
Ausgangsproblem auf eine Folge linearer Programme zurückgeführt wird.
durch konvexe Polyeder, womit das
Ausgangsproblem auf eine Folge linearer Programme zurückgeführt wird.
Zunächst wird ein Polyeder
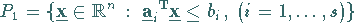 |
(18.109) |
bestimmt.
Aus dem linearen Programm
 |
(18.110) |
wird ein bezüglich 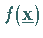 optimaler Eckpunkt
optimaler Eckpunkt 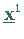 von
von 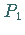 erhalten.
Ist
erhalten.
Ist 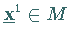 ,
dann ist die Optimallösung des Ausgangsproblems gefunden.
Anderenfalls wird eine Hyperebene
,
dann ist die Optimallösung des Ausgangsproblems gefunden.
Anderenfalls wird eine Hyperebene
die den Punkt 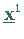 von
von 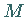 trennt,
ermittelt, so daß das neue Polyeder
trennt,
ermittelt, so daß das neue Polyeder
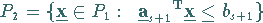 |
(18.111) |
erhalten wird.
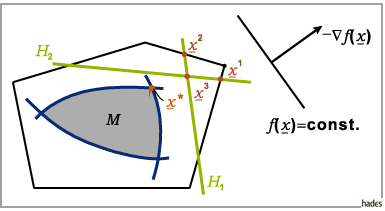
Die Abbildung zeigt eine schematische Darstellung des Schnittebenenverfahrens.
![]() gelöst wird.
gelöst wird.
![]() in
der Nähe des Minimalpunktes
in
der Nähe des Minimalpunktes ![]() durch konvexe Polyeder, womit das
Ausgangsproblem auf eine Folge linearer Programme zurückgeführt wird.
durch konvexe Polyeder, womit das
Ausgangsproblem auf eine Folge linearer Programme zurückgeführt wird.
![]() optimaler Eckpunkt
optimaler Eckpunkt ![]() von
von ![]() erhalten.
Ist
erhalten.
Ist ![]() ,
dann ist die Optimallösung des Ausgangsproblems gefunden.
Anderenfalls wird eine Hyperebene
,
dann ist die Optimallösung des Ausgangsproblems gefunden.
Anderenfalls wird eine Hyperebene