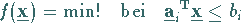|
|
|
|
 |
(18.94) |
mit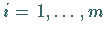 
.
Eine zulässige Abstiegsrichtung 
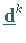im Punkt 
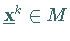wird auf
folgende Weise ermittelt:
Ist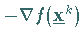 
eine zulässige Richtung, dann wird
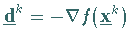gesetzt.
Anderenfalls liegt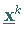 
auf dem Rand von 
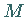und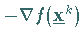
zeigt
aus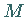
hinaus.
Mittels einer linearen Abbildung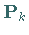 
wird der Vektor
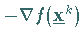auf eine lineare Teilmannigfaltigkeit des Randes von
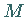projiziert, die von einer
Teilmenge der in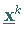
aktiven Restriktionen gebildet wird.
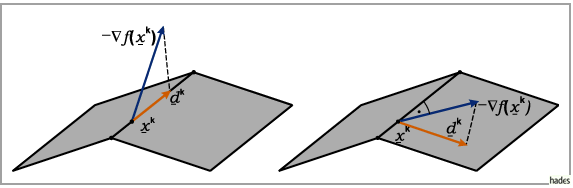
Die Projektion auf eine Kante zeigt die folgende linke Abbildung, die Projektion auf eine
Seitenfläche die rechte Abbildung.
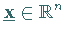sind die Vektoren 
,
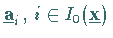linear unabhängig, ist eine solche Projektion gegeben durch
 |
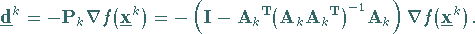(18.95) |
Dabei besteht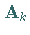 
aus allen den 
,
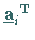deren
entsprechende Nebenbedingungen die lineare Teilmannigfaltigkeit bilden, in die
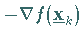projiziert werden soll.
|
|