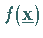|
|
|
|
ist genau dann konvex (streng konvex), wenn die Matrix
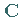positiv semidefinit (positiv definit) ist.
Alle Aussagen über konvexe Optimierungsprobleme können für quadratische Aufgaben
mit positiv semidefiniter Matrix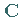
übertragen werden, insbesondere ist die
SLATER-Bedingung immer erfüllt, und deshalb ist für die Optimalität eines
Punktes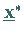 
notwendig und hinreichend, daß ein Punkt
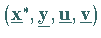existiert, der das entsprechende System der
lokalen KUHN- TUCKER-Bedingungen erfüllt.
|
|