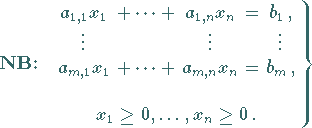Formulierung mit vorzeichenbeschränkten Variablen und Schlupfvariablen
Für die Herleitung eines Lösungsverfahrens ist es günstig, das System der
Nebenbedingungen (18.1b; 18.2b) als Gleichungssystem mit
vorzeichenbeschränkten Variablen zu schreiben.
Dazu wird jede freie Variable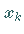 
durch die Differenz von jeweils zwei nichtnegativen
Variablen 
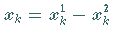ersetzt.
Die Ungleichungsbedingungen werden durch Addition einer nichtnegativen Variablen, der
Schlupfvariablen , in Gleichungen überführt.
Damit nimmt das lineare Optimierungsproblem die folgende Form an:
Die Kurzform lautet:
 |
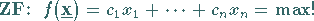(18.4a) |
 |
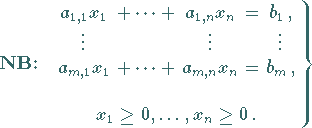(18.4b) |
 |
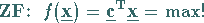(18.5a) |
 |
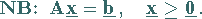(18.5b) |
Es kann vorausgesetzt werden, daß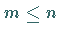 
,
da anderenfalls das
Gleichungssystem linear abhängige bzw. widersprüchliche Gleichungen enthält.
