Themen dieser Seite
Konvexe Aufgabe wird die Optimierungsaufgabe
 |
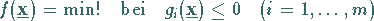(18.42) |
genannt, wenn die Funktionen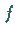 
und 
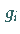konvex sind.
Insbesondere können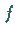
und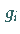
lineare Funktionen sein.
Für konvexe Aufgaben gilt:
a) Jedes lokale Minimum von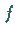
über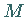 
ist auch globales Minimum.
b) Ist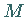
nicht leer und beschränkt, dann existiert mindestens eine Lösung
von (18.42).
c) Ist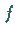
streng konvex, dann existiert höchstens eine Lösung von
(18.42).
Optimalitätsbedingungen
a) Ist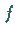
stetig partiell differenzierbar, dann ist 
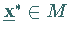genau
dann Lösung von (18.42), wenn gilt:
 |
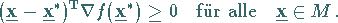(18.43) |
b) Die SLATER-Bedingung
ist eine Regularitätsbedingung für den zulässigen Bereich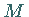 
.
Sie ist erfüllt, wenn ein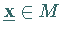 
mit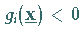 
für alle nicht
affin linearen Funktionen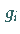
existiert.
c) Ist die SLATER-Bedingung erfüllt, dann ist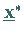 
genau dann ein
Minimalpunkt von (18.42), wenn ein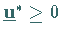 
existiert, so daß
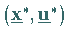ein Sattelpunkt der LAGRANGE-Funktion ist.
Sind darüber hinaus die Funktionen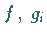 
differenzierbar, dann ist
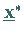genau dann eine Lösung von (18.42), wenn
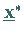den lokalen
KUHN- TUCKER-Bedingungen genügt.
d) Für ein konvexes Optimierungsproblem mit differenzierbaren Funktionen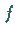
und
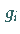kann das duale Problem (18.41a,b) einfacher formuliert werden:
Der Gradient von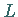 
wird hier nur bezüglich 
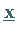gebildet.
e) Für konvexe Optimierungsaufgaben gilt der starke Dualitätsatz :
Erfüllt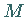
die SLATER-Bedingung und ist
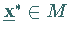eine Lösung von
(18.42), dann existiert ein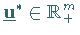 
,
so daß
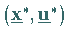eine Lösung des dualen Problems (18.44a,b) ist,
und es gilt:
 |
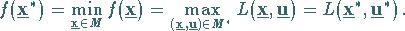(18.45) |
