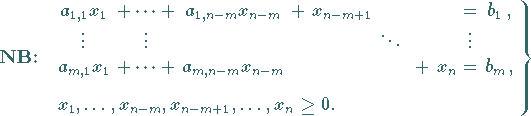Normalform und Basislösung
Die lineare Optimierungsaufgabe kann immer, eventuell durch Umbenennung der Variablen,
folgendermaßen umgeformt werden:
 |
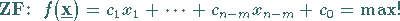(18.8a) |
 |
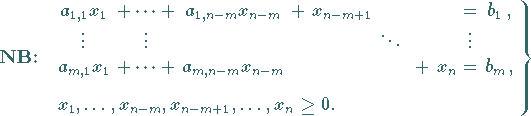(18.8b) |
Die letzten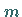 
Spalten der Koeffizientenmatrix sind offensichtlich linear unabhängig
und bilden eine Basis.
Die Basislösung
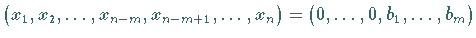kann sofort aus dem Gleichungssystem abgelesen werden.
Ist 
,
dann heißt (18.8a,b) eine Normalform
oder kanonische Form des linearen Optimierungsproblems .
In diesem Falle ist die Basislösung zulässig, d.h., sie ist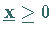 
,
und
somit eine Ecke von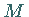 
.
In der Normalform bezeichnet man die Variablen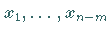 
als
Nichtbasisvariable und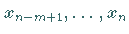 
als Basisvariable .
Der zur Ecke gehörende Zielfunktionswert ist 
,
da die in der Zielfunktion
auftretenden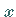 
-Komponenten, die Nichtbasisvariablen, verschwinden.
