Definition der Ecke und Satz über die Ecke
1. Definition der Ecke
Ein Punkt 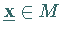 heißt Ecke von
heißt Ecke von 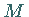 ,
wenn für alle
,
wenn für alle
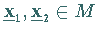 mit
mit 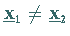 gilt:
gilt:
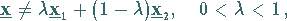 |
(18.7) |
d.h., 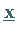 liegt nicht auf der Verbindungsgeraden zweier verschiedener Punkte aus
liegt nicht auf der Verbindungsgeraden zweier verschiedener Punkte aus
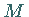 .
.
2. Satz über den Eckpunkt
Der Punkt 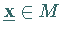 ist genau dann ein Eckpunkt von
ist genau dann ein Eckpunkt von 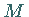 ,
wenn
die zu den positiven Komponenten von
,
wenn
die zu den positiven Komponenten von 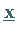 gehörenden Spalten der Matrix
gehörenden Spalten der Matrix
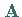 linear unabhängig sind.
linear unabhängig sind.
Unter der Annahme, daß der Rang von 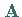 gleich
gleich 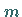 ist, können nur
maximal
ist, können nur
maximal 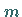 Spalten von
Spalten von 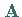 linear unabhängig sein.
Deshalb kann ein Eckpunkt höchstens
linear unabhängig sein.
Deshalb kann ein Eckpunkt höchstens 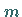 positive Komponenten besitzen.
Die restlichen
positive Komponenten besitzen.
Die restlichen 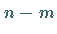 Komponenten sind gleich Null.
Im Normalfall sind genau
Komponenten sind gleich Null.
Im Normalfall sind genau 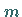 Komponenten positiv.
Ist die Anzahl der positiven Komponenten jedoch kleiner als
Komponenten positiv.
Ist die Anzahl der positiven Komponenten jedoch kleiner als 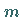 ,
dann spricht man von
einer entarteten Ecke .
,
dann spricht man von
einer entarteten Ecke .
![]() gleich
gleich ![]() ist, können nur
maximal
ist, können nur
maximal ![]() Spalten von
Spalten von ![]() linear unabhängig sein.
Deshalb kann ein Eckpunkt höchstens
linear unabhängig sein.
Deshalb kann ein Eckpunkt höchstens ![]() positive Komponenten besitzen.
Die restlichen
positive Komponenten besitzen.
Die restlichen ![]() Komponenten sind gleich Null.
Im Normalfall sind genau
Komponenten sind gleich Null.
Im Normalfall sind genau ![]() Komponenten positiv.
Ist die Anzahl der positiven Komponenten jedoch kleiner als
Komponenten positiv.
Ist die Anzahl der positiven Komponenten jedoch kleiner als ![]() ,
dann spricht man von
einer entarteten Ecke .
,
dann spricht man von
einer entarteten Ecke .