Eigenschaften linearer Optimierungsprobleme
An Hand des obigen Beispiels können einige Eigenschaften linearer
Optimierungsprobleme graphisch veranschaulicht werden.
Dazu kann auf die Einführung von Schlupfvariablen
verzichtet werden.
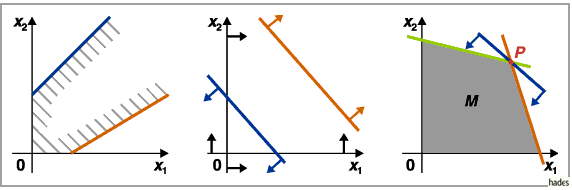
a) Eine Gerade 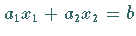 teilt die
teilt die 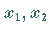 -Ebene in zwei
Halbebenen.
Somit liegen alle Punkte
-Ebene in zwei
Halbebenen.
Somit liegen alle Punkte 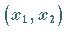 ,
die die Ungleichung
,
die die Ungleichung 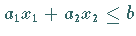 erfüllen, auf dieser Geraden bzw. in einer der Halbebenen.
Die graphische Darstellung der Punktmenge in einem kartesischen Koordinatensystem erfolgt
durch Einzeichnen der trennenden Geraden, und die Halbebene, die die Lösungsmenge der
Ungleichung enthält, wird mit Pfeilen gekennzeichnet.
Die Ausführung der graphischen Darstellung aller Nebenbedingungen liefert eine Menge
von Halbebenen, deren Durchschnitt den zulässigen Bereich
erfüllen, auf dieser Geraden bzw. in einer der Halbebenen.
Die graphische Darstellung der Punktmenge in einem kartesischen Koordinatensystem erfolgt
durch Einzeichnen der trennenden Geraden, und die Halbebene, die die Lösungsmenge der
Ungleichung enthält, wird mit Pfeilen gekennzeichnet.
Die Ausführung der graphischen Darstellung aller Nebenbedingungen liefert eine Menge
von Halbebenen, deren Durchschnitt den zulässigen Bereich 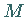 bildet (s. Abbildung).
bildet (s. Abbildung).
Im Beispiel oben bilden die Punkte von  eine Polygonfläche.
Es kann auch vorkommen, daß
eine Polygonfläche.
Es kann auch vorkommen, daß  unbeschränkt oder leer ist.
Treffen in einer Ecke des Polygons mehr als zwei begrenzende Geraden aufeinander, dann
spricht man von einer entarteten Ecke (s. folgende Abbildung).
unbeschränkt oder leer ist.
Treffen in einer Ecke des Polygons mehr als zwei begrenzende Geraden aufeinander, dann
spricht man von einer entarteten Ecke (s. folgende Abbildung).
b) Alle Punkte in der 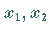 -Ebene, die der Beziehung
-Ebene, die der Beziehung
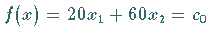 genügen, liegen auf einer gemeinsamen Geraden, der
Niveaulinie zum Funktionswert
genügen, liegen auf einer gemeinsamen Geraden, der
Niveaulinie zum Funktionswert  .
Bei verschiedener Wahl von
.
Bei verschiedener Wahl von  wird eine Schar paralleler Geraden definiert, auf denen
der Zielfunktionswert jeweils konstant ist.
Geometrisch sind alle diejenigen Punkte Lösungen des Optimierungsproblems, die sowohl
zum zulässigen Bereich
wird eine Schar paralleler Geraden definiert, auf denen
der Zielfunktionswert jeweils konstant ist.
Geometrisch sind alle diejenigen Punkte Lösungen des Optimierungsproblems, die sowohl
zum zulässigen Bereich 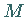 als auch zu einer Niveaulinie
als auch zu einer Niveaulinie 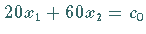 mit
einem maximalen
mit
einem maximalen 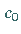 gehören.
Im konkreten Fall ergibt sich auf der Niveaulinie
gehören.
Im konkreten Fall ergibt sich auf der Niveaulinie 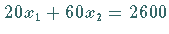 der
Maximalpunkt
der
Maximalpunkt 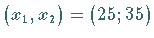 .
Die Niveaulinien sind in der folgenden Abbildung dargestellt, wobei die Pfeile in die
Richtung wachsender Funktionswerte zeigen.
.
Die Niveaulinien sind in der folgenden Abbildung dargestellt, wobei die Pfeile in die
Richtung wachsender Funktionswerte zeigen.
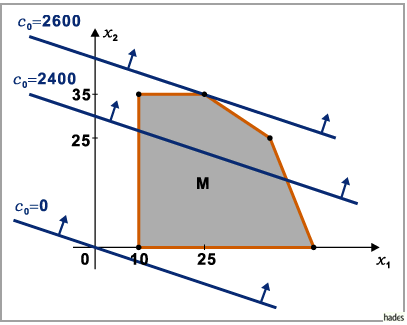
Man erkennt, daß bei beschränktem zulässigen Bereich 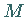 das Maximum in mindestens
einer Ecke von
das Maximum in mindestens
einer Ecke von 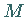 eingenommen wird.
Dagegen ist bei unbeschränktem
eingenommen wird.
Dagegen ist bei unbeschränktem 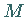 denkbar, daß der Zielfunktionswert gegen
unendlich strebt.
denkbar, daß der Zielfunktionswert gegen
unendlich strebt.