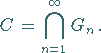Fraktale

Fraktale

Attraktoren oder andere invariante Mengen von dynamischen Systemen können geometrisch komplizierter als Punkt, Linie oder Torus aufgebaut sein. Fraktale sind, auch unabhängig von einer Dynamik, Mengen, die sich durch eines oder mehrere Merkmale wie Ausfransung, Porösität, Komplexität, Selbstähnlichkeit auszeichnen. Da der übliche Dimensionsbegriff, wie er für glatte Flächen und Kurven gebraucht wird, für Fraktale nicht anwendbar ist, müssen verallgemeinerte Definitionen der Dimension herangezogen werden. Eine ausführlichere Darstellung der Dimensionstheorie s. Lit. 17.9, 17.5.

Beispiel

Das Intervall 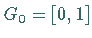wird in drei Teilintervalle gleicher Länge geteilt und das mittlere offene Drittel entfernt, so daß die Menge

entsteht. Dann werden von den beiden Teilintervallen von 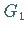die jeweils mittleren offenen Drittel entfernt, so daß die Menge

entsteht. Diese Prozedur wird mit 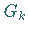fortgesetzt, indem aus jedem Teilintervall von 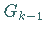das mittlere offene Drittel entfernt wird. Dadurch entsteht eine Folge von Mengen

wobei jede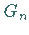s aus 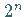Intervallen der Länge 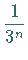besteht. Die CANTOR-Menge 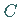ist definiert als Menge aller der Punkte, die allen 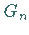angehören, d.h.,

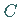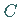Die Menge ist kompakt, überabzählbar, hat das LEBESGUE-Maß Null und ist perfekt. D.h., ist abgeschlossen, und jeder Punkt ist Häufungspunkt. Die CANTOR-Menge kann als Beispiel für ein Fraktal dienen.