Definition der topologischen Konjugiertheit
Gegeben sei neben (17.3) ein weiteres diskretes System
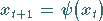 |
(17.24) |
mit 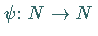 ,
wobei
,
wobei 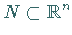 eine beliebige Menge
und
eine beliebige Menge
und 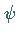 stetig ist (
stetig ist (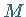 und
und 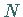 können auch allgemein metrische Räume sein).
Die diskreten Systeme (17.3) und (17.24)
(bzw. die Abbildungen
können auch allgemein metrische Räume sein).
Die diskreten Systeme (17.3) und (17.24)
(bzw. die Abbildungen 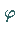 und
und 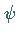 )
heißen topologisch konjugiert ,
wenn ein Homöomorphismus ( konjugierender Homöomorphismus )
)
heißen topologisch konjugiert ,
wenn ein Homöomorphismus ( konjugierender Homöomorphismus )
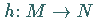 existiert, so daß
existiert, so daß 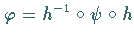 ist.
Sind (17.3) und (17.24) topologisch konjugiert,
so überführt der konjugierende Homöomorphismus
ist.
Sind (17.3) und (17.24) topologisch konjugiert,
so überführt der konjugierende Homöomorphismus 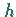 die Orbits von
(17.3) in Orbits von (17.24).
die Orbits von
(17.3) in Orbits von (17.24).