Chaos in eindimensionalen Abbildungen
Für stetige Abbildungen eines kompakten Intervalls in sich gibt es zahlreiche
hinreichende Bedingungen für die Existenz chaotischer invarianter Mengen.
Drei Beispiele sollen genannt werden.
1. Satz von Shinai:
Sei 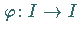 eine stetige Abbildung eines kompakten Intervalls
eine stetige Abbildung eines kompakten Intervalls
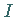 (z.B.
(z.B. 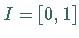 )
in sich.
Dann ist das System
)
in sich.
Dann ist das System 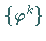 auf
auf 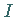 genau dann chaotisch im Sinne von
DEVANEY, wenn die topologische Entropie von
genau dann chaotisch im Sinne von
DEVANEY, wenn die topologische Entropie von 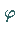 auf
auf 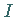 ,
d.h.
,
d.h. 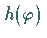 ,
positiv ist.
,
positiv ist.
2. Satz von Sharkovsky:
Die positiven ganzen Zahlen seien folgendermaßen geordnet:
Sei 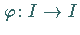 eine stetige Abbildung eines kompakten Intervalls
in sich und habe
eine stetige Abbildung eines kompakten Intervalls
in sich und habe 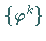 auf
auf 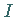 einen
einen 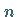 -periodischen Orbit.
Dann hat
-periodischen Orbit.
Dann hat 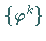 auch einen
auch einen 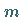 -periodischen Orbit, wenn
-periodischen Orbit, wenn 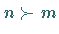 ist.
ist.
3. Satz von Block, Guckenheimer und Misiuriewicz:
Sei 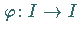 eine stetige Abbildung des kompakten Intervalls
eine stetige Abbildung des kompakten Intervalls
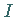 in sich, so daß
in sich, so daß 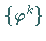 einen
einen 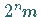 -periodischen Orbit
(
-periodischen Orbit
(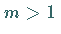 ,
ungerade) besitzt.
Dann ist
,
ungerade) besitzt.
Dann ist 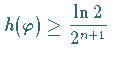 .
.
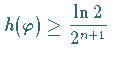 .
.