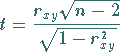Test auf Unabhängigkeit zweier Merkmale
Bei praktischen Aufgaben ist zu untersuchen, ob eine Stichprobe, die aus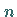 
Meßpunkten 
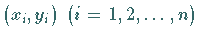besteht, aus einer
zweidimensionalen, normalverteilten Grundgesamtheit mit dem Korrelationskoeffizienten
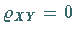stammt, so daß die beiden Zufallsgrößen 
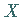und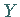 
als
unabhängig angesehen werden können.
Der Test läuft wie folgt ab:
1. Aufstellen der Hypothese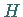 
:
.
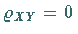2. Vorgabe einer Irrtumswahrscheinlichkeit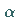 
und Ermittlung des Quantils
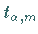aus der Tabelle t-Verteilung für 
.
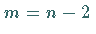3. Berechnung der Testgröße
 |
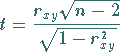(16.155a) |
mit
 |
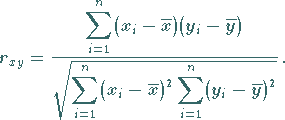(16.155b) |
4. Ablehnung der Hypothese, falls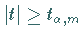 
ist.
Die Größe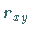 
heißt empirischer Korrelationskoeffizient .
