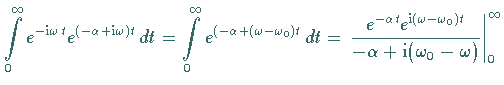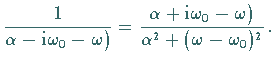Bildfunktion einer gedämpften Schwingung: Die in der folgenden linken Abbildung
dargestellte gedämpfte Schwingung wird durch die Funktion
 |
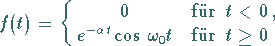(15.99a) |
beschrieben.
Zur Vereinfachung der Rechnung wird die FOURIER-Transformation der komplexen
Funktion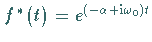 
ermittelt.
Es gilt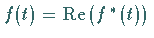 
.
Die FOURIER-Transformation liefert:
Das Ergebnis ist die LORENTZ- oder BREIT-WIGNER-Kurve
 |
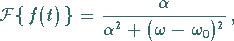(15.99c) |
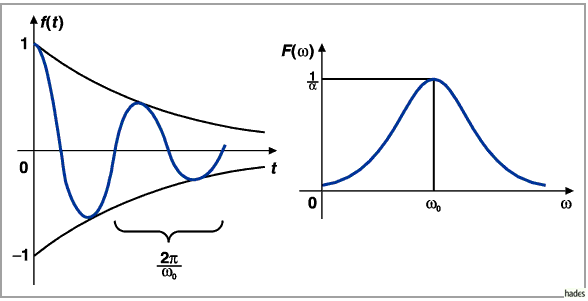
die in der rechten Abbildung dargestellt ist.
Einer gedämpften Schwingung im Zeitbereich entspricht ein einziger Peak im
Frequenzbereich.
