Umkehrtransformationen
In den Anwendungen ist die Rücktransformation einer Bildfunktion in die Originalfunktion
von unmittelbarem Interesse.
Man spricht auch von Umkehrtransformation oder inverser Transformation .
Bei Benutzung des Symbols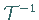 
schreibt sich die Umkehrung der
Integraltransformation (15.1b) gemäß
 |
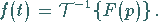(15.2a) |
Der Operator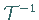
heißt der zu 
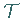inverse Operator , so
daß gilt:
 |
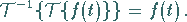(15.2b) |
Die Bestimmung der Umkehrtransformation bedeutet, die Lösung der Integralgleichung
(15.1a) zu suchen, in der die Funktion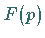 
gegeben ist und die Funktion
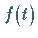gesucht wird.
Wenn eine Lösung existiert, kann sie in der Form
 |
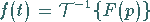(15.2c) |
geschrieben werden.
Die explizite Bestimmung der inversen Operatoren für die verschiedenen
Integraltransformationen, d.h. für verschiedene Kerne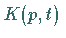 
,
gehört zu den
grundlegenden Problemen der Theorie der Integraltransformationen.
Der Anwender benutzt zur Lösung seiner Probleme vor allem die in entsprechenden
Tabellen angegebenen Korrespondenzen von zusammengehörigen Bild- und
Originalfunktionen (Tabellen
LAPLACE-Transformationen,
FOURIER-Kosinus-Transformationen,
FOURIER-Sinus-Transformationen,
FOURIER-Transformationen,
Exponentielle FOURIER-Transformationen und
Z-Transformationen).
